Unlocking Algebra (WIP)

Foreword

Hi anon! Congratulations on being curious and dropping your ego :) I created this article solely to solidify my intuitive understanding of algebra by explaining it in public.

Mathematics is the gateway to further understanding the universe and the biggest enabler in the current world in conjunction with programming. I was always hesitant to learn it because I never saw its potential. Now, after committing to pursuing AI, I see its power and hope to rub off this passion I’ve developed for it. It explains dynamic changes, relationships, algorithms, and everything we can see and think of can be represented with math. It’s a tool only the trained can wield where the world morphs into its true self.

Rant over. The reason behind this is that I’m incredibly curious to see what kind of explanatory power differential geometry and differential equations hold. The intuitive understanding of the following topics is of the same importance as multiplication/division and addition/subtraction in the non-linear world, and thus why it’s a must to understand intuitively. This article is merely a way to truly understand and reference when I slip up, as a cue mechanism to remind my neurons to stop forgetting (if they do).

All-in-all, I hope this helps you in some way, through inspiration or by learning something :)

---

Mathematics is the abstract science of measure and number.

A number is composed of units, whether these are whole or fractional parts, rather than strictly being a multiple of whole units.

A fraction is a number apart of another number. A smaller number that measures a larger one either as a whole or through its parts.

Algebra sacrifices the 100% precision of geometry for generality. Therefore, algebra is a weaker form of geometry.

Vocab

The things you sum together are called terms. The things that multiply with each other are called factors.

Whenever we have a set we say an item, e.g., x, is a part of the set we use the in notation denoated as $$x \in \{ ... \}$$

If we have 2 sets,

$$A = \{ 1, 2 \}$$ $$B = \{ 1, 3 \}$$

The combination of both sets, or union, would be denoted with a cup symbol. Think of it as all the unique items in the sets are scooped up.

$$A \cup B = \{ 1, 2, 3 \}$$

The inverse is the intersection. What are overlapping items in both sets? Think of it as spill all the non-duplicate items,

$$A \cap B = \{ 1 \}$$

You’ll end up seeing these things very often so it’s good to understand them early on!

Equilibrium

If you understand this one rule the entirety of mathematical manipulation will begin to click: You may modify the equation as long as both sides are still equal.

This means you can do anything as long as the equilibrium is true.

For example,

$$\begin{split} a + 1 &= \dfrac{b}{1} \\[1em] a + 1 \color{red}{-1} &= \dfrac{b}{1} \color{red}{-1} \\[1em] &= \dfrac{b}{1} - \dfrac{1}{1} \\[1em] &= \dfrac{b - 1}{1} \\[1em] \end{split}$$

What we do on one side we do to the other to maintain equilibrium!

The goal is to transform the equation while maintaining its truth value. Every step should result in an equation that is equivalent to the original.

Fractions

Fractions can be seen with the perspective of [number][type]. To give you an idea what I mean heres an example [1][million] + [2][million] = [3][million]. When we think of adding fractions together we would say [1][forth] + [2][forths] = [3][forths] aka $\dfrac{1}{4} + \dfrac{2}{4} = \dfrac{3}{4}$. Then if we try to add 2 things like [1][forth] + [2][thirds] = ? we notice that they aren’t the same type…So we must make them the same type by factoring, using both original denominators to create a new number, e.g., 3 * 4 = 12 and then multiplying the numberators by the opposite number, so 2/3 becomes 2(4)/3(4) and then we can use that notation of [number][twelfths]! Easy as pie!

Another example could be [number][x^2] + [number][x^2], the same principle applies!

Factoring is quite interesting. It’s the lowest set numbers used to create another number, e.g, 12 = { 2, 2, 3 } because 2 * 2 = 4 and 4 * 3 = 12.

An example of fractions would be,

$$\begin{split} \dfrac{3x}{\sqrt{x}} &= \dfrac{3x}{\sqrt{x}} \cdot \dfrac{\sqrt{x}}{\sqrt{x}} \\[1em] &= \dfrac{3x\sqrt{x}}{(\sqrt{x})^2} \\[1em] &= \dfrac{3x\sqrt{x}}{x} \\[1em] &= \dfrac{3 \cdot \cancel{x} \sqrt{x}}{\cancel{x}} \\[1em] &= 3\sqrt{x} \\ \end{split}$$

Underlying Syntax Meaning

It may seem obvious but you need to remember that something like 3x = 3 * x.

This comes in clutch when dealing with something like this:

We start by inversing the negative exponent,

$$\begin{split} \dfrac{3x^{-2}}{x^4} &= \dfrac{3 \cdot \dfrac{1}{x^{2}}}{x^4} \\[1em] &= \dfrac{\dfrac{3}{1} \cdot \dfrac{1}{x^{2}}}{x^4} \\[1em] &= \dfrac{\dfrac{3\cdot 1}{1 \cdot x^{2}}}{x^4} \\[1em] &= \dfrac{\dfrac{3}{x^{2}}}{x^4} = \dfrac{\dfrac{3}{x^{2}}} {\color{red}\dfrac{x^4}{1}} \\[2.5em] \end{split}$$

We multiply by the reciprocal to get rid of the denominator in the complex fraction

$$\begin{split} &= \dfrac{3}{x^{2}} \color{red}{\cdot \dfrac{1}{x^4}} \\[1em] &= \dfrac{3 \cdot 1}{x^2 + x^4} \\[1em] &= \dfrac{3}{x^{2 + 4}} \\[1em] \end{split}$$

Cross Multiply

When encountering something like,

$$\begin{split} \dfrac{10}{4} = \dfrac{x + 6}{6} \end{split}$$

And then hearing “cross-multiply” what they’re saying is to get the $\dfrac{10}{4}$ to the other side of the equation then you have to multiply itself by its reciprocal (inverse) $\dfrac{4}{10}$ to remove it from the left side then do the same to the right side to maintain equilibrium.

$$\begin{split} {\color{red}{\dfrac{4}{10}}} \cdot \dfrac{10}{4} &= \dfrac{x + 6}{6} \cdot {\color{red}{\dfrac{4}{10}}} \\[1em] 1 &= \dfrac{4(x+6)}{10(6)} \\[1em] &= \dfrac{4x+24}{60} \\[1em] {\color{red}{60}} \cdot 1 &= \dfrac{4x+24}{\cancel{60}} \cdot \cancel{\color{red}{60}} \\[1em] 60 &= 4x+24 \\[1em] {\color{red}{(-24)}} + 60 &= 4x + 24 + {\color{red}{(- 24)}} \\[1em] \dfrac{36}{4} &= x \\[1em] 9 &= x \\[1em] \end{split}$$

Alternative Routes

There are many ways to solve equations, but only a deep understanding of the fundamentals allows you to go off and figure out how to. As long as you abide by the rules of mathematics you can do anything, remember?

So an alternative way to solving the above is,

$$\begin{split} \dfrac{3x^{-2}}{x^4} &= 3 \cdot \dfrac{x^{-2}}{x^4} \\ &= 3 \cdot x^{-2-4} \\ &= 3 \cdot x^{-6} \\ &= 3 \cdot \dfrac{1}{x^6} \\[1em] &= \dfrac{3}{1} \cdot \dfrac{1}{x^6} \\[1em] &= \dfrac{3}{x^6} \\[1em] \end{split}$$

---

Fractions

When we think of the number

$$2$$

We usually think it’s a single number, which is true!

However, when we visualise it as a fraction we represent it as

$$2 = \dfrac{2}{1}$$

Because, how many 2s go into 1? Itself, right?

And so when thinking about

$$2 + 3$$

We’re saying

$$\begin{split} 2 + 3 &= \dfrac{2}{1} + \dfrac{3}{1} \\[1em] &= \dfrac{5}{1} \\[1em] &= 5 \end{split}$$

Reduce To Lowest Terms

To visually see how we cancel out and simplify rationals let me show you an example,

$$\begin{split} \dfrac{21}{45} &= \dfrac{7 \cdot \cancel{3}}{5 \cdot 3 \cdot \cancel{3}} \\[1em] &= \dfrac{7}{15} \\[1em] \end{split}$$

Or by factoring the GCF,

$$\begin{split} \dfrac{3x + 6}{x^2 + 4x + 4} &= \dfrac{3 \cancel{ (x + 2) } }{ \cancel{(x+2)}(x+2) } \\[1em] &= \dfrac{3}{x+2} \\[1em] \end{split}$$

Multiplying & Dividing

$$\begin{split} \dfrac{\dfrac{4}{5}}{\dfrac{2}{3}} &= \dfrac{4}{5} \cdot \dfrac{3}{2} \\[1em] &= \dfrac{4 \cdot 3}{5 \cdot 2} \\[1em] &= \dfrac{12}{10} \\[1em] &= \dfrac{\cancel{2} \cdot 6}{\cancel{2} \cdot 5} \\[1em] &= \dfrac{6}{5} \\[1em] \end{split}$$

Add & Sub

Simple Example

This is a bit more complicated bc we have to have a common denominator (preferred least common denominator) to apply to add or sub. They need to be the same type of programming.

Lets start easy,

$$\begin{split} \dfrac{7}{6} - \dfrac{4}{15} \end{split}$$

We can get the common denominator by $6 \cdot 15 = 90$ but we want the least common denominator,

$$\begin{split} 6 &= 2 \cdot 3 \\ 15 &= 3 \cdot 5 \\ \end{split}$$

And so we get every element once of this set, $$\{ x | x \in \{ 2, 3, 3, 5 \} \} = \{ 2, 3, 5 \}$$ creating $$LCD = 2 \cdot 3 \cdot 5 = 30$$

Then to get our rationals to become equal we must multiply the denominators by their missing factors,

$$\begin{split} \dfrac{7}{6} \cdot \dfrac{5}{5} - \dfrac{4}{15} \cdot \dfrac{2}{2} &= \dfrac{35}{30}-\dfrac{8}{30} \\[1em] &= \dfrac{27}{30} \\[1em] &= \dfrac{3^3}{2 \cdot 3 \cdot 5} \\[1em] &= \dfrac{3^2}{2 \cdot 5} \\[1em] &= \dfrac{9}{10} \\[1em] \end{split}$$

Complex Example

Let’s do a more complex one:

$$\begin{split} \dfrac{3}{2x+2} + \dfrac{5}{x^2 - 1} \end{split}$$

The LCD is found by

$$\begin{split} 2x + 2 &= 2(x + 1) \\ x^2 - 1 &= (x + 1)(x - 1) \\ \end{split}$$

which is

$$2(x + 1)(x - 1)$$

Then we multiply our denominators by whatever parts of the LCD they are missing

$$\begin{split} \dfrac{3}{2x+2} \cdot {\color{red}{ \dfrac{x-1}{x-1} }} + \dfrac{5}{x^2 - 1} \cdot \color{red} \dfrac{2}{2} &= \dfrac{3(x-1)+10}{2(x+1)(x-1)} \\[1em] &= \dfrac{3x - 3 + 10}{2(x + 1)(x - 1)} \\[1em] &= \dfrac{3x + 7}{2(x+1)(x - 1)} \\[1em] \end{split}$$

Rational Equations

Standard

Now that we have the rules of rationals down, we can try to solve

$$\begin{split} \dfrac{x}{x + 3} = 1 + \dfrac{1}{x} \\[1em] \end{split}$$

First, we find the LCD. Since the denominators have no factors in common we simply multiply them together to get

$$LSD = (x+3)x$$

Then we multiply the LSD to both sides to make the types the same, allowing us to clear the denominator,

$$\begin{split} ((x+3)x)\dfrac{x}{x + 3} &= 1 + ((x+3)x) \left(1 + \dfrac{1}{x} \right) \\[1em] \cancel{(x+3)} (x)\dfrac{x}{\cancel{x + 3}} &= 1 + (x+3)(x) \cdot 1 + (x+3)\cancel{(x)} \cdot \dfrac{1}{\cancel{x}} \\[1em] \cancel{x^2} &= \cancel{x^2} + 3x + x + 3 \\ 0 &= 4x + 3 \\ -3 &= 4x \\ \dfrac{-3}{4} &= x \\[1em] \end{split}$$

Killing off the denominator is the entire point of multiplying each rational with the LCD. You multiply by something that removes them so you no longer deal with the denominators.

Sometimes you’ll get an extraneous solution, meaning an x makes a denominator in the original equation going to 0. You don’t use it and hopefully the other x will work.

Fracitonal Exponent

We now have the intuition for exponents down. But there is a slight trick to increase our intuition. Solve,

$$\begin{split} 2p^{\frac{4}{5}} = \dfrac{1}{8} \end{split}$$

First, we isolate the part of the equation w/ the fractional exponent

$$\begin{split} { \color{red}{ \dfrac{1}{2} } } \cdot 2p^{ \frac{4}{5} } &= \dfrac{1}{8} \cdot \color{red}\dfrac{1}{2} \\[1em] p^{ \frac{4}{5} } &= \dfrac{1}{16} \\[1em] \end{split}$$

Then we get rid of the fractional exponent

$$\begin{split} (p^{\frac{4}{5}})^{\color{red}{5}} = \left( \dfrac{1}{16} \right)^{\color{red}{5}} \\[1em] p^{\frac{4}{\cancel{5}} \cdot \cancel{5}} &= \left( \dfrac{1}{16} \right)^5 \\[1em] p^4 &= \left( \dfrac{1}{16} \right)^5 \\[1em] (p^4)^{\frac{1}{4}} &= \pm \left( \left( \dfrac{1}{16} \right)^5 \right)^{\frac{1}{4}} \\[1em] p^{4 \cdot \frac{1}{4}} &= \pm \left( \left( \dfrac{1}{16} \right)^5 \right)^{\frac{1}{4}} \\[1em] p &= \pm \left( \dfrac{1}{16} \right)^{\frac{5}{4}} \\[1em] &= \pm \left( \sqrt[4]{ \dfrac{1}{16} } \right)^5 \\[1em] &= \pm \left( \dfrac{\sqrt[4]{1}}{\sqrt[4]{16}} \right)^5 \\[1em] &= \pm \left( \dfrac{1}{2} \right)^5 \\[1em] &= \pm \dfrac{1^5}{2^5} \\[1em] &= \pm \dfrac{1}{32} \\[1em] \end{split}$$

Then you check your answers to see if any make the denominator 0, to which you don’t include it in your solution set.

---

Different Denominators

But what if we had different denominators?

$$\begin{split} \dfrac{2}{3} + \dfrac{3}{5} \end{split}$$

Then we find the common factor between the two, meaning what number do both 3 and 5 create that they share? [3, 6, 9, 12, 15] for 3 and [5, 10, 15] for 5, therefore we multiply both to get them to the 15 denominator. And of course, whatever you do to the bottom you must do to the top to make them equal.

$$\begin{split} 5\left(\dfrac{2}{3}\right) + 3\left(\dfrac{3}{5}\right) &= \dfrac{5(2)}{5(3)} + \dfrac{3(3)}{3(5)} \\[1em] &= \dfrac{10}{15} + \dfrac{9}{15} \\[1em] &= \dfrac{10 + 9}{15} \\[1em] &= \dfrac{19}{15} \\[1em] \end{split}$$

---

Multiplying Fractions

What if we had

$$\begin{split} \dfrac{3}{5} \cdot \dfrac{6}{3} \end{split}$$

Then we can simplify the right fraction since there are 2 3s in 6.

$$\begin{split} \dfrac{3}{5} \cdot 2 \end{split}$$

This is also represented as

$$\begin{split} \dfrac{3}{5} \cdot \dfrac{2}{1} \end{split}$$

Which gives us

$$\begin{split} \dfrac{3 \cdot 2}{5 \cdot 1} &= \dfrac{6}{5} \end{split}$$

---

Dividing Fractions

What if we had a fraction divided by another fraction (a complex fraction)?

Let’s start by dividing two real numbers.

$$\begin{split} 6 \div 2 &= \dfrac{6}{2} \\ &= 3 \\ \end{split}$$

When we apply the same logic to two fractions we get

$$\dfrac{2}{7} \div \dfrac{3}{5} = \dfrac{\left(\dfrac{2}{7}\right)}{\left(\dfrac{3}{5}\right)}$$

And then we multiply the denominator by its inverse to turn it into a 1.

Remember, we must apply to the top what we do to the bottom

$$\dfrac{ \left( \dfrac{2}{7} \textcolor{red}{\cdot \dfrac{5}{3}} \right) }{ \cancel{ \left( \dfrac{3}{5} \textcolor{red}{\cdot \dfrac{5}{3}} \right) } }$$

And then we’re left w/

$$\dfrac{2}{7} \cdot \dfrac{5}{3} = \dfrac{10}{21}$$

---

Reciprocals

When moving a term from one side of the equation to another we need to keep equilibrium to do so. With fractions, the concept of the reciprocal is to “reciprocate” or mean the same thing when moving it. This means whatever we do on one side we must do the opposite on the other side.

With fractions we want to = 1.

$$\dfrac{3}{5}(x) = y$$

The way we cancel out the fraction on the left side is by multiplying it by its inverse and then doing the same on the other side, as so:

$$\begin{split} \cancel { \textcolor{red}{\dfrac{5}{3} \cdot }\dfrac{3}{5} } (x) &= \textcolor{red}{\dfrac{5}{3}}(y) \\[1em] \textcolor{red}{1} (x) &= \dfrac{5}{3}(y) \\[1em] x &= \dfrac{5}{3}(y) \\[1em] \end{split}$$

To continue, let’s use the reciprocal in a complex fraction. To switch the division sign to multiplication we must inverse the fraction too.

$$\begin{split} \dfrac{\left(\dfrac{x}{11}\right)}{y} &= \dfrac{x}{11} \div \dfrac{y}{1} \\[1em] &= \dfrac{x}{11} \cdot \dfrac{1}{y} \\[1em] &= \dfrac{x}{11y} \\[1em] \end{split}$$

---

Exponents

Exponents are replicating machines. The number n represents how many times we double our base b, e.g. $b^n$ means we multiply b by itself n times.

Intuition

When thinking of exponents we must think of the area of a shape. The power of two is the area of a 2-dimensional shape represented w/ $x^2$ (e.g., a square), three dimensions are $x^3$ (e.g. a cube) and so on. The reason we use squares for measuring is because the decimals of accuracy are infinitesimal vs. a regular whole number such as 2. This is why powers are regularly for accurate measurement.

Zero Exponent

What if we have an exponent of 0?

$$2^0$$

We intuitively think of exponents as for each +1 to n in $2^n$ there is another copy of the base, in this case, 2, e.g.,

$$\begin{split} 2^1 = 2\\ 2^2 = 2 \cdot 2 \\ \end{split}$$

Remember, to remove multiplication we must divide and so to subtract an n we must divide by the base.

So we can do the following

$$\begin{split} 2^1 = 2^{2-1} &= 2 \cdot 2 \textcolor{red}{\div 2} \\ &= 2 \cdot \dfrac{2}{\textcolor{red}2} \\ &= 2 \cdot 1 \\ &= 2 \end{split}$$

Now using this logic, you’ll notice what happens when we visualise the 0 exponent

$$\begin{split} 2^0 = 2^{1-1} &= 2 \textcolor{red}{\div 2} \\[.5em] &= \dfrac{2}{\textcolor{red}2} \\[.5em] &= 1 \\ \end{split}$$

Negative Exponents

We know that a positive exponent is the base multiplied by itself n times,

$$\begin{split} 2^3 = 2 \cdot 2 \cdot 2 \end{split}$$

So what is the inverse of an exponent, what is the opposite of multiplication? Division!

Therefore, a negative exponent is the same as the base divided by itself n times,

$$2^{-3} = 2 \div 2 \div 2$$

We can extend this intuition further with

$$2^{-3} = \dfrac{1}{2^{3}}$$

Let me show you how to prove it!

By using the product rule we get the 0 exponent, 1,

$$\begin{split} 2^{3} \cdot 2^{-3} &= 2^{3 + (-3)} \\ &= 2^0 \\ &= 1 \\ \end{split}$$

And since we know 1 can be ditto’ed into anything we can say,

$$1 = \dfrac{2^3}{2^3}$$

We therefore can use our knowledge of mathematical equilibrium to modify this equation,

$$\begin{split} 2^{3} \cdot 2^{-3} &= 1 \\[1em] \dfrac{\cancel{2^3} \cdot 2^{-3}}{\cancel{\color{red}2^3}} &= \dfrac{1}{\color{red}2^3} \\[1em] 2^{-3} &= \dfrac{1}{2^3} \\[1em] \end{split}$$

We can think of negative exponents in the numerator as positive exponents in the denominator and vice versa!. Think of it as a transaction: you pay the opposite of what you are to move to the other side.

---

Adding Exponents

You should have noticed that

$$\begin{split} 2^2 \cdot 2^4 &= 4 \cdot 16 \\ &= 64 \\ 2^2 \cdot 2^4 &= 2^{2+4} \\ &= (2 \cdot 2) \cdot (2 \cdot 2 \cdot 2 \cdot 2) \\ &= 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \\ &= 2^6 \\ &= 64 \end{split}$$

---

Quotient Property

It turns out that when we subtract 2 exponents of the same base then it’s the same as dividing them! Let me show you with a proof

$$\begin{split} 3^4 - 3^2 &= 3^{4 - 2} \\ &= \dfrac{3^4}{3^2} \\[1em] &= \dfrac{3 \cdot 3 \cdot \cancel{\color{red}{3 \cdot 3}}}{\cancel{\color{red}{3 \cdot 3}}} \\[1em] &= 3^2 \\ &= 9 \\ \end{split}$$

Therefore, we can conclude that

$$\begin{split} b^n - b^m = b^{n-m} = \dfrac{b^n}{b^m} \end{split}$$

---

Distributing Exponents

If we had

$$\begin{split} (2 + 3)^2 &\not= 2^2 + 3^2 \\ &\not= 4 + 9 \\ &= (2 + 3)(2 + 3) \\ &= (2 \cdot 2) + (2 \cdot 3) + (3 \cdot 2) + (3 \cdot 3) \\ &= 24 \\ \end{split}$$

You cannot distribute an exponent over add or sub because the exponent means multiply the parentheses n times. If it was division or multiplication inside we could distribute.

For example,

$$\begin{split} (2 \cdot 3)^2 &= 2 \cdot 2 \cdot 3 \cdot 3 \\ &= 4 \cdot 9 \\ &= 36 \\ (2 \cdot 3)^2 &= (6)^2 \\ &= 36 \\ \end{split}$$

---

Properties

There is an interesting property when it comes to exponents, being able to reverse engineer the base b with the exponent’s reciprocal!

$$b^n = a \longleftrightarrow b = a^{\frac{1}{n}}$$

How do we get to this point?

We took the root of the fraction (the exponential reciprocal).

We can use the exponential power rule,

$$(b^n)^m = b^{nm}$$

to prove this equality

$$\begin{split} b &= a^{\frac{1}{n}} \\ (b)^n &= (a^{\frac{1}{n}})^n \\ b^n &= a^{\frac{n}{n}} \\ &= a^{1} \\ &= a \\ \end{split}$$

---

Roots/Radicals

To continue with intuition we need to know what roots are.

These are the opposite of exponents, just as division is the opposite of multiplication. But instead of positive and negative exponents, it’s inversing the fraction. This is why the exponent rules apply to radicals. E.g.,

$$\begin{split} \sqrt{2 - 1} & \not = \sqrt{2} - \sqrt{1} \\ & \not = -1+\sqrt{2} \\ &= \sqrt{-1} \\ &= 1 \end{split}$$

Roots solve for the base (b), using the exponent n and the result!

For something like,

$$\sqrt[3]{8}$$

We read this as: “What number when multiplied by itself 3 times gives me 8?”

$$\begin{split} 2^3 &= 2 \cdot 2 \cdot 2 \\ &= 8 \end{split}$$

If we know what the result is and the exponent that was used we can find the base, in this case 2.

$$\begin{split} \sqrt[3]{8} &= 8^{\frac{1}{3}} \\ &= 2 \end{split}$$

But what is the intuition behind the exponent of $\dfrac{1}{3}$?

$$\begin{split} ( 8^{ \frac{1}{3} } )^3 &= 8^{ \frac{1}{3} \cdot 3 } \\ &= 8^{ \frac{1}{3} \cdot \frac{3}{1} } \\ &= 8^{ \frac{1 \cdot 3}{3 \cdot 1} } \\ &= 8^{ \frac{3}{3} } \\ &= 8^1 \\ &= 1 \cdot 8 \\ &= 8 \\ \end{split}$$

---

Another way to view roots:

$$\begin{split} 3 &= \sqrt[3]{27} \\ &= \dfrac{1}{(3)^2}(27) \\[1em] &= \dfrac{1}{9}(27) \\[1em] \end{split}$$

---

Root Exponent

If we wanted to take the sqr of x^5 then the exponent will be the top of the fraction reciprocal.

$$\begin{split} \sqrt{x^5} &= \dfrac{5}{2}x \end{split}$$

Intuition

What if we had

$$\begin{split} a^{\frac{m}{n}} &= a^{\frac{m}{1} \cdot \frac{1}{n}} \\ &= a^{m \cdot \frac{1}{n}} \\ &= (a^{m})^{\frac{1}{n}} \\ &= \sqrt[n]{a^m} \\ \end{split}$$

Now I’m going to go back 1 step and go an alternative route just to show some intuition

$$\begin{split} &= (a^{m})^{\frac{1}{n}} \\ &= (a^{\frac{1}{n}})^m \\ &= (\sqrt[n]{a})^m \\ &= (\sqrt[n]{a})^m \\ \end{split}$$

We can swatch the m and the fraction because they’re going to equal the same thing regardless of the order.

Let’s do an example,

$$\begin{split} 25^{\frac{-3}{2}} &= \dfrac{1}{25^\frac{3}{2}} \\[1em] &= \dfrac{1}{(\sqrt{25})^3} \\[1em] &= \dfrac{1}{5^3} \\[1em] &= \dfrac{1}{125} \\[1em] \end{split}$$

Geometric Intuition

The intuition goes further. What actually is $\sqrt{2}$? That is, what is the number that when multiplied itself results in 2? Well, we know that $x^2$ is the area of a square. Therefore, to discover what creates the area of our square, 2, we need to have all four sides be equal to $\sqrt{2}$. This intuition goes beyond this 2nd dimensional power into fractional exponents, 3, 4, 5, etc. We may not be able to conceive of them perceptually but they do indeed exist.

---

Logarithms

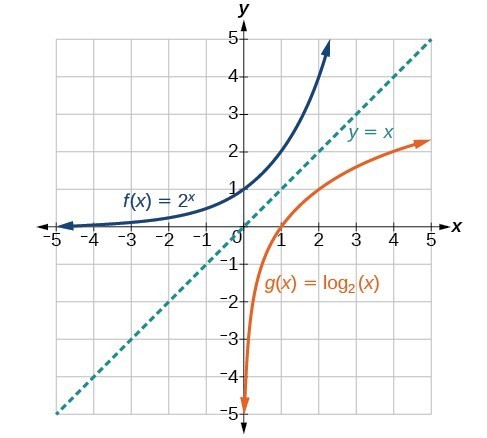
Logarithms ask: What exponent should the base have to get the input?

An example that will spark the intuition from our roots and fractional exponents is,

$$\begin{split} \log_{2}{\dfrac{1}{8}} &= \dfrac{1}{2^3} \\[1em] &= 2^{-3} \\[1em] \end{split}$$

We can see from this graph that g(x) represents the log graph. It can never to a negative x because there is no exponent that can result in a negative number, and the same with 0.

Another example is,

$$\log_{10}(1,000) = 3 = \dfrac{3}{1}$$

Meaning we multiply 10 by itself 3 (10 * 10 * 10) times to get 1_000.

Software engineers use mostly

$$\log_2(x)$$

because they work in binary, 1 or 0!

Intuition

The best intuition is this:

$$\begin{split} \sqrt{8} &= \sqrt{4 \cdot 2} \\ &= \sqrt{4} \cdot \sqrt{2} \\ &= 2 \cdot \sqrt{2} \\ &= \pm 2\sqrt{2}\\ \end{split}$$

We do the plus minus because both the positive and negative versions of a number multiplied themselves will create the pre-rooted number.

---

When we think of these two variables, lets think of them as normal variables x, then we can say we have 2 of them but remembering how exponents act when multiply two powers we actually add them together

$$\begin{split} 2^2 \cdot 2^3 &= 2^{2 + 3} \end{split}$$

We use the reverse logic with logs bc they’re the inverse of exponents. So when adding two logs we actually multiply them, to get the product. And when we think of x^2 it’s really two lots of x which is why we are able to put the 2 in front of the log.

$$\begin{split} \log_a{x} + \log_a{x} &= \log_a(x \cdot x) \\ &= \log_a(x^2) \\ &= 2 \log_a(x) \\ \end{split}$$

We cannot have logs of 0 or negative numbers because there is no base to the exponent of n that can even create 0 or a negative number. It’s impossible!

If the input of a log is a fraction then the output will always be a negative number, since we’re scaling down. If the base is larger than the input then the output will be a fraction and the opposite is true for a whole number as the output.

What if the bases are different?

$$\begin{split} \log_a{x} + \log_b{x} &= \end{split}$$

Well if addition converts to multiplication then subtraction must correspond to division!

$$\begin{split} \log_a{x} - \log_a{x} &= \log_a(x \div x) \\[1em] &= \log_a \left( \dfrac{x}{x} \right) \\[1em] &= 1 \\[1em] \end{split}$$

But what if the log bases are different?

$$\begin{split} \log_a{x} - \log_b{x} &= \dfrac{\log_a(x)}{\log_b(x)} \\[1em] \end{split}$$

Log Types

Natural log, e, represents 10. Why 10 though? It makes scaling the magnitude of things simple allowing for getting down to decimals extremely easy or scaling up to building lengths intuitively easy.

A log of base 2 represnts bits in computers, 0 and 1, which are 2 types. So whenever we deal with bytes (8 bits) we can scale up and down. Its the digitalised version of the natural log.

Essentially, these common logs are catered for the field of use to make management of the underlying measurements a lot easier intuitively for decimal precision.

---

What if we swapped the base and the result?

$$\log_{1,000}(10) = \dfrac{1}{3}$$

We get the inverse exponent.

Since we know the original log = 3 we can actually replace 3 with $\log_{10}(1,000)$ to create

$$\log_{1,000}(10) = \dfrac{1}{log_{10}(1,000)}$$

Pretty fascinating stuff, eh?

---

So, we know roots solve for the base b, but when we have the base and the result logarithms allow us to solve for the exponent n.

For example, if we had

$$2^5 = 32$$

Then the inverse would be

$$\log_2{(32)} = 5$$

because the function of the log is: how many times does the base 2 have to be multiplied by itself to result in our input, 32?

In this case, we have to multiply our base, 2 by itself 5 times to make 32.

---

What if we had the following?

$$\log_2{1}$$

We’re asking how many times we have to double 2 to get its original value. To which we get = 0 since we don’t need to double it at all to get it to its size.

But then what happens if we go into fractions, such as

$$\log_2{\left(\dfrac{1}{2}\right)}$$

Well, we can think about how the following exponent works,

$$\begin{split} 2^1 &= 2 \\ &= \dfrac{2}{1} \end{split}$$

And so if we inverse the 1 into -1 then we get the reciprocal (opposite)

$$\begin{split} 2^{-1} &= \dfrac{1}{2^{1}} \\ \end{split}$$

---

Equality

Given the following

$$\begin{split} \log_10(12x - 7) &= \log_10(3x + 11) \end{split}$$

Do you notice something?

The exact same symbol of $\log_10$ is on both sides. This means we can dropped them on both sides bc if we subtract a log from on side we do it to the other and therefore removing from both sides!

Leaving us with

$$\begin{split} 12x - 7 &= 3x + 11 \\ 12x &= 3x + 18 \\ 9x &= 18 \\ x &= 2 \end{split}$$

But we have to check our answer bc sometimes it doesn’t actually create an equality! So lets do that

$$\begin{split} \log_10(12x - 7) &= \log_10(3x + 11) \\ \log_10(12(2) - 7) &= \log_10(3(2) + 11) \\ \log_10(24 - 7) &= \log_10(6 + 11) \\ \log_10(17) &= \log_10(17) \\ \end{split}$$

In this case it was correct! It’s not a negative number (which is impossible to solve bc exponents can never make a negative) and it’s equal!

Product Property

Similar to exponent product rule logs have the same property.

If we have something like

$$\begin{split} \log_2(4) + \log_2(2) &= 3 \\ 2 + 1 &= 3 \\ \end{split}$$

And we can prove our product rule by converting the log into an exponent

$$\begin{split} \log_2(4) + \log_2(2) &= 3 \\ \log_2(4 \cdot 2) &= 3 \\ 4 \cdot 2 &= {\color{red}{2}}^3 \\ 8 &= 8 \end{split}$$

Power Property

There is an interesting property with logs where you can convert the input’s exponent into a multiplcation outside of the log, like,

$$\begin{split} 2 \cdot \log_2(4) &= 2 \cdot 2 \\ &= 4 \\ 2 \cdot \log_2(4) &= \log_2(4^2) \\ &= \log_2(16) \\ &= 4 \\ \end{split}$$

Quotient Property

Similar to the exponent property we can follow the last proof with the new feature of combining like logs to form a singular log!

$$\begin{split} \log_2(16) - \log_2(4) &= 4 - 2 \\ &= 2 \\ \log_2(16) - \log_2(4) &= \log_2 \left( \dfrac{16}{4} \right) \\[1em] &= \log_2 \left( \dfrac{2^4}{2^2} \right) \\[1em] &= \log_2 ( 2^2 ) \\ &= \log_2 ( 2^2 ) \\ &= \log_2 ( 4 ) \\ &= 2 \end{split}$$

Therefore the quotient rule is exactly the same as the exponent one but w/ the same log being the encasulator!

Change Of Base Property

We usually use this when we want to convert an uncommon base into the core base we normally use in our respected fields, i.e., IRL = base 10, computers = base 2, etc. So when we have log base 3 for architecture IRL we want to convert it to the natural log because it’s much easier to work with for measurement w/ 10s over 3s!

So how do we do this?

$$\begin{split} x &= \log_a(b) \\ \end{split}$$

Then we convert the log into exponent form

$$\begin{split} a^x &= b \\ \log_c(a^x) &= \log_c(b) \\ x \cdot \log_c(a) &= \log_c(b) \\ \dfrac{x \cancel{\cdot \log_c(a)}}{\cancel{\log_c(a)}} &= \dfrac{\log_c(b)}{\log_c(a)} \\ \end{split}$$

Adding Logs

Let’s think of

$$\log_2{16}$$

It’s asking, what is n in $2^n = 16$?

Let me show you two ways this intervention applies

$$\begin{split} \log_2{16} &= \log_2{4} + \log_2{4} \\ &= 2 + 2 \\ &= 4 \end{split}$$

And

$$\begin{split} \log_2{(16)} &= \log_2{(4)} + \log_2{(4)} \\ &= \log_2{(4 \cdot 4)} \\ &= \log_2{(4^2)} \\ &= 2\log_2{(4)} \\ &= 2(2) \\ &= 4 \end{split}$$

The reason we don’t add the logs as

$$\begin{split} \log_2{(16)} &= \log_2{(4)} + \log_2{(4)} \\ &\not= \log_2{(8)} \\ \end{split}$$

is because

$$\log_2{(8)} = 3 \not = \log_2{(16)} = 4$$

It’s a bit counter-intuitive at face value. Hopefully, this clears it up!

---

Factoring

Factoring is by far the most common thing you’ll be doing in algebra. It’s what simplifying an equation is all about. Turn these massive term pieces of shit into simple elegant eye candies!

Greatest Common Factor

The greatest common factor (GCF) is the largest thing that divides each term, e.g,

$$\begin{split} 15 + 25x &= \dfrac{15 + 25x}{5} \\ &= 3 + 5x \\ \end{split}$$

These are our secondary factored terms, so now we put the GCF 5 as a distributer encasing them, i.e.,

$$\begin{split} = 5(3+5x) \end{split}$$

Factor By Grouping

If there are 4 terms, so a 3rd-degree polynomial, then we can section them by factoring with the GCF for the left pair and the right pair. E.g.,

$$\begin{split} \color{red}{x^3 + 3x^2} + 4x + 12 &= \color{red}{x^2(x+3)} + 4(x+3) \\ &= \color{red}{(x^2 + 4)}(x + 3) \end{split}$$

Factor Quadratics

The intuition is a bit unusual but if you have

$$\begin{split} (d^2 - 9) = (d + 3)(d - 3) \end{split}$$

because if you see a negative then …

If it were to be

$$\begin{split} h^2 + 4h + 3 = (h + 3)(h + 1) \end{split}$$

If we have something like

$$\begin{split} 10x^2 + 11x - 6 \end{split}$$

and cannot immediately find the factors of what adds up to 11 and multiplies into -6 so we end up multiplying 10 * 6 = 60 and solve for adding up to

#	Adds to 11	Multiplies to 60
1	-1	60
2	-2	30
3	-3	20
4	-4	15

We find our solution w/ -4 and 15!

Now we can convert our quadratic

$$\begin{split} 10x^2 + 11x - 6 &= 10^2 - 4x + 15x - 6 \\ &= 2x(5x - 2) + 3(5x - 2) \\ &= (2x + 3)(5x - 2) \\ \end{split}$$

Completing The Square

Difference Of Squares

If we have something like

$$\begin{split} 9x^2 - 1 &= (3p)^2 - (1)^2 \\ &= (3p + 1)(3p - 1) \\ \end{split}$$

There is no formula for the sum of squares bc it cannot be factored further!

Let’s try a trickier example,

$$\begin{split} w^2 &= 121 \\ w^2 - 121 &= 0 \\ w^2 - \pm \sqrt{121} &= 0 \\ w^2 - \pm 11 &= 0 \\ (w + 11)(w - 11) &= 0 \\ w &= \{ -11, 11 \} \end{split}$$

Remember that whenever you square root a non-negative even number you get a plus-minus bc a negative multiplied by another negative of itself creates a positive too! An odd non-negative would only have a single solution.

Difference Of Cubes

$$\begin{split} a^3 - b^3 = (a-b)(a^2 + ab + b^2) \end{split}$$

The sum is the inverse sign for the first and second term and then positive down the line

$$\begin{split} a^3 + b^3 = (a+ b)(a^2 - ab + b^2) \end{split}$$

Cannot Factor?

What if we had something we couldn’t factor all the way, such as:

$$\begin{split} x(x+2) &= 7 \\ x^2 + 2x &= 7 \\ x^2 + 2x - 7 = 0 \\ \end{split}$$

Then our only option is to use the quadratic formula

$$\begin{split} x &= \dfrac{-2 \pm \sqrt{ 2^2 - 4(1)(-7) } }{ 2(1) } \\[1em] &= \dfrac{-2 \pm \sqrt{32} }{2} \\[1em] &= \dfrac{-2 \pm \sqrt{ 16 \cdot 2} }{2} \\[1em] &= \dfrac{-2 \pm \sqrt{16} \sqrt{2} }{2} \\[1em] &= \dfrac{-2 \pm 4 \sqrt{2} }{2} \\[1em] &= \dfrac{-2}{2} \pm \dfrac{4 \sqrt{2} }{2} \\[1em] &= -1 \pm \dfrac{4 \sqrt{2} }{2} \\[1em] \end{split}$$

I want to show another example using rationals as coefficients

$$\begin{split} \dfrac{1}{2}y^2 &= \dfrac{1}{3}y - 2 \\[1em] \dfrac{1}{2}y^2 - \dfrac{1}{3}y + 2 &= 0 \\[1em] \end{split}$$

At this point, we can remove the denominators by using them to multiply everything!

$$\begin{split} 0 &= \dfrac{1}{2}y^2 - \dfrac{1}{3}y + 2 \\[1em] &= \left( 2 \cdot 3 \right) \left( \dfrac{1}{2}y^2 - \dfrac{1}{3}y + 2 \right) \\[1em] &= 6 \left( \dfrac{1}{2}y^2 - \dfrac{1}{3}y + 2 \right) \\[1em] &= 3y^2 - 2y + 12 \end{split}$$

Then we use the quadratic equation!

---

Quadratics

Standard Form

Let’s start by converting a vertex form into a standard form quadratic

$$\begin{split} f(x) &= -4(x - 3)^2 + 1 \\ &= -4(x^2 -6x + 9) + 1 \\ &= -4x^2 +24x - 35 \\ \end{split}$$

Vertex Form

Let’s convert this standard form quadratic into vertex form,

$$\begin{split} g(x) &= 2x^2 + 8x + 6 \end{split}$$

First, we need to find the x value of the vertex w/ the formula

$$\begin{split} \dfrac{-b}{2a} &= \dfrac{-8}{2(2)} \\[1em] &= -2 \end{split}$$

The vertex’s x formula $\dfrac{-b}{2a}$ comes from the quadratic formula

$$\begin{split} \dfrac{{\color{red}{-b}} \pm \sqrt{b^2 - 4ac}}{\color{red}{2a}} \end{split}$$

And then to get our y value we plug that x value into g(x)

$$\begin{split} g(-2) &= 2(-2)^2 + 8(-2) + 6 \\ &= 8 - 16 + 6 \\ &= -2 \\ \end{split}$$

So the quadratic in vertex form is

$$\begin{split} g(x) &= a(x - h)^2 + k \\ &= a(x - (-2))^2 + (-2) \\ &= a(x + 2)^2 - 2 \\ \end{split}$$

And since our coefficient needs to be the same as the original standard form we replace a = 2.

---

End

This was my first, although small, article on mathematics. I’ll be writing more as I progress in my mathematical career to understand deeper. If you have any comments, concerns, etc, feel free to get in contact with me!

Thanks for reading, anon.