Understanding Quadratics (WIP)

What Are Quadratics

Quadratics are second degree polynomials identified by the squared exponent $ax^2$ in

$$y = ax^2 + bx + c$$

This is where the term “quadratic” comes from. “quad,” meaning square, because the variable is squared.

These equations are the gateway drug into the world of non-linearity. A quadratic is a U-shaped curve called a parabola. Depending on the sign of $a$, the parabola opens upwards ($a > 0$) or downwards ($a < 0$).

Syntax Breakdown

Firstly, the quadratic coefficient $a$ is what determines the parabolas direction (opening upwards if $a > 0$ and downwards if $a < 0$) and it’s width (a larger $|a|$ makes it narrower and a smaller $|a|$ widens it).

The linear coefficient $b$ impacts the horizontal x position of the parabola, and thus the vertex along the x-axis and the symmetry of the parabola.

The constant term $c$ is the y-intercept of the parabola, the point where the graph crosses the y-axis. This can be any part of the parabola, not just the vertex!

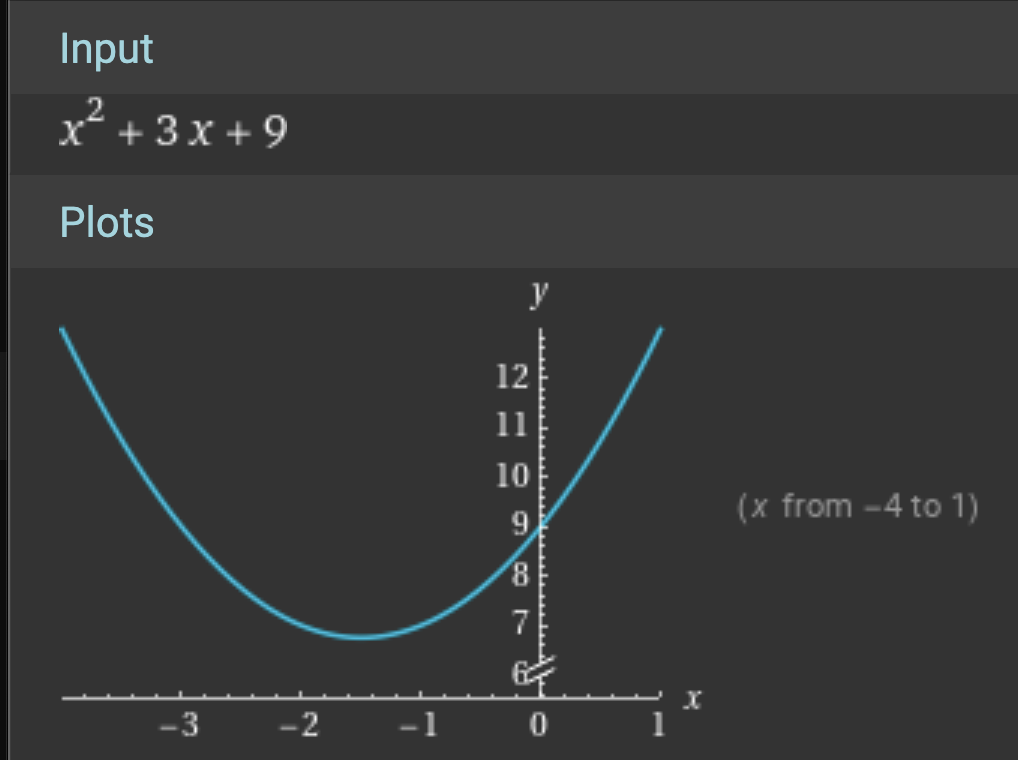
As you can see w/ this example the right side of the parabola intercepts the y-axis at c = 9

Vertex

The highest or lowest point on the parabola is called the vertex. A vertical line can be drawn through the vertex to indicate the axis of symmetry: where the left side of the parabola is reflected on the right side.

Roots

We solve for the x-values we call the roots where the parabola intersects the x-axis where the function equals 0. This can be either 0, 1 or 2. 0 where the axis isn’t touched at all, 1 where only the vertex touches the x-axis and 2 where the vertex is below the x-axis, causing 2 distinct points to be intersected.

To determine the roots we either use factoring, completeting the square, or the quadratic formula, which we’ll go over shortly.

Discriminant

…

---

Why Quadratics?

For any problem that is in a single dimension and not linear then we’d use quadratics. A perfect example that is heavily used in AI for minimising functions is gradient descent! With this we keep adjusting our value to get closer to the vertex by assessing the tangent of our coordinates.

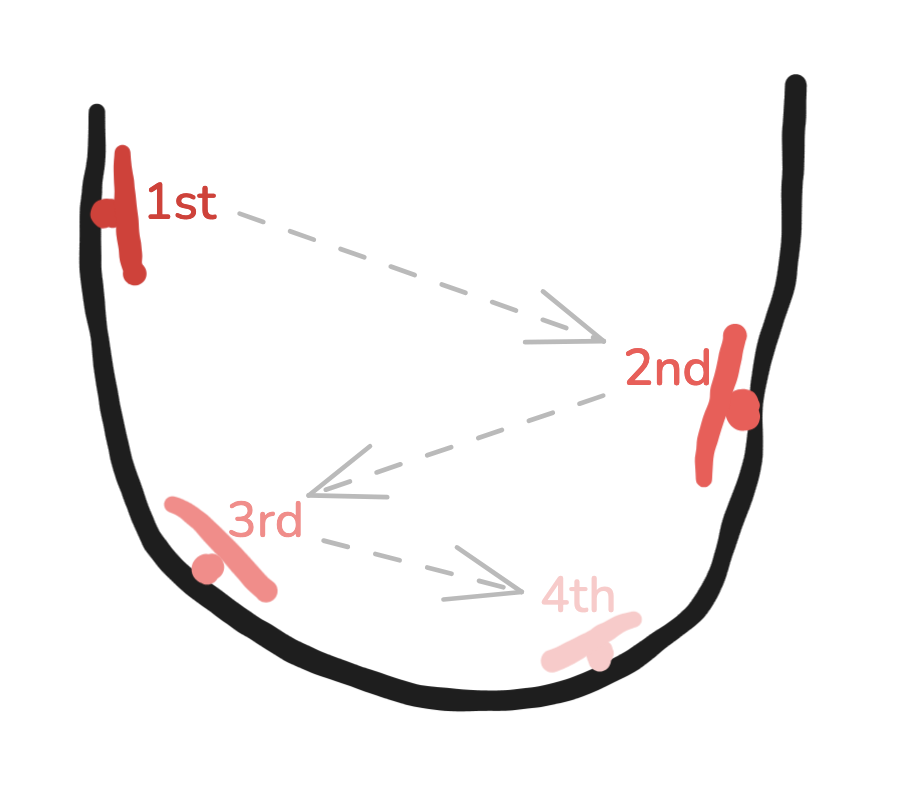
For example, this following graph represents how we minimise a quadratic, convex problem. Lets say we start at the 1st point and notice that the tangent line tells us decreasing our value is how we get closer to the global minimum and since it’s so steep we use a larger number to change our value.

This overshoots but gets closer to the global min but now our tangent has switched so we increase our value by a little bit and we reach the 3rd point. Then we keep repeating this process until our tanget of the point we land on is, or very close, to being horizontal.

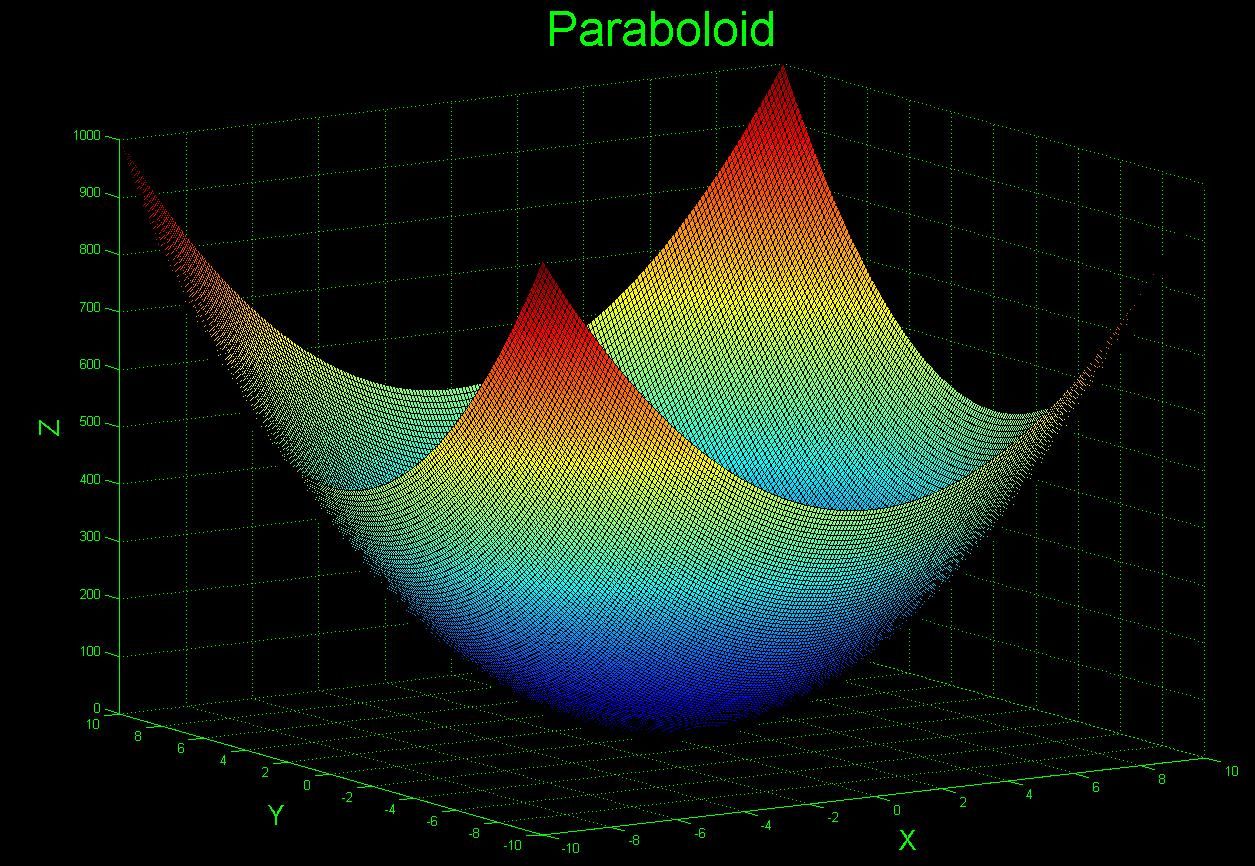
When we get into the multi-dimensional world we’ll encounter objects like a paraboloid where we would try and optimise to get to the lowest point of it. Since there is only a single minimum point we know it’s a convex problem and can use quadratics!

Anything non-convex means there’s no longer a single minimum but multiple, which we label local (not the lowest we can go) and global minimum (lowest we can possibly go). This is where the representation of optimising multi-variable systems, cough AI, would come into play.

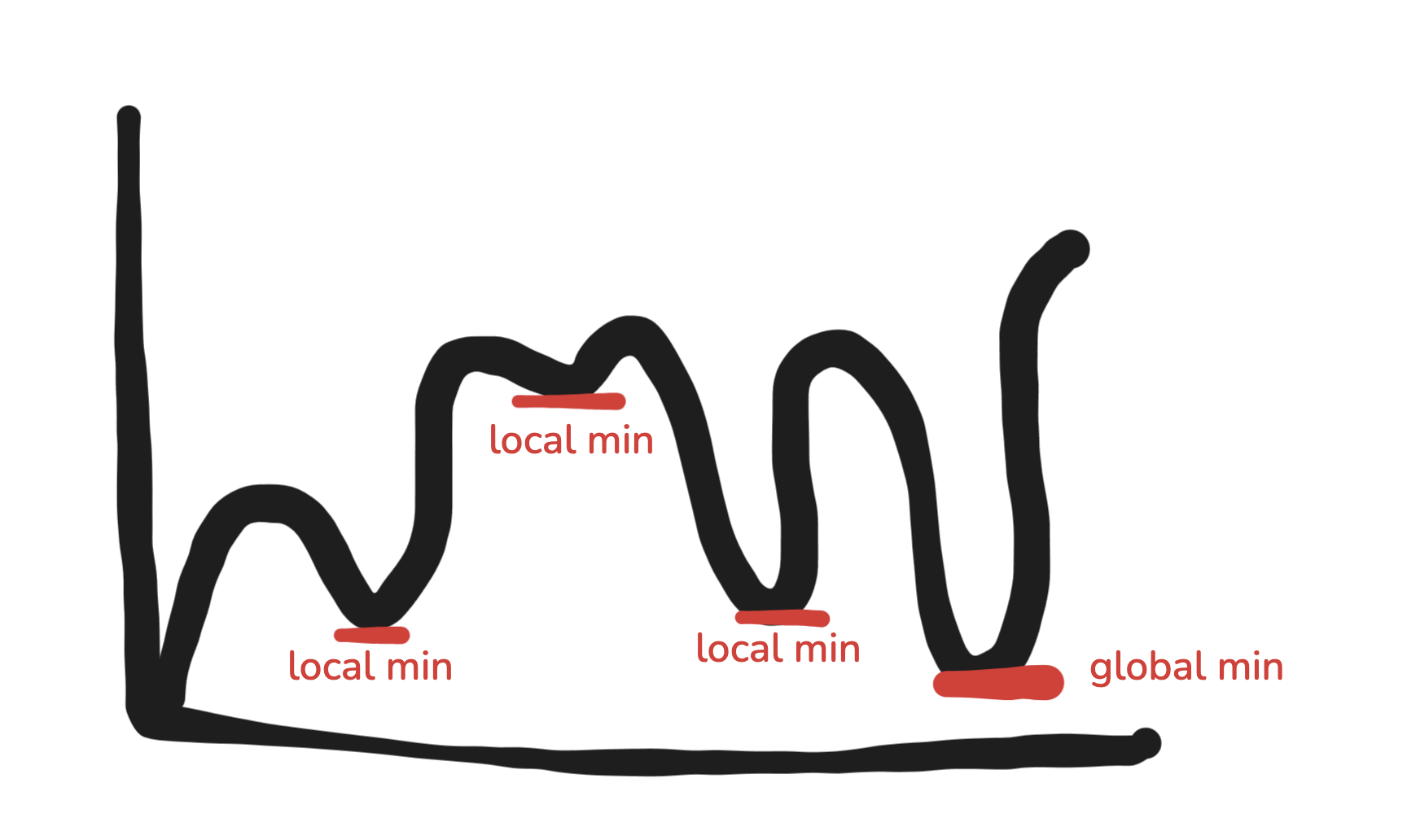
And so obviously, we need to truly understand quadratic systems before we can go into the realm of non-convex systems. Don’t worry, anon. There are tons of opportunities to apply convex optimising, especially in finance. This is like our gateway drug into calculus!

---

Factoring

Easy

Lets say we for the general quadratic formula

$$ax^2 + bx + c$$

have the following quadratic

$$x^2 + 4x -12$$

To factor it we must find two numbers that have the multiplicative sum of c, -12 and additive sum of b, 4.

Our options for multiplication start from 1 and end at 3:

#	Multiples of 12	Additive Sum
1	$1 \cdot (-12)$	$1 + (-12) = -11$
2	$(-1) \cdot 12$	$(-1) + 12 = 11$
3	$2 \cdot (-6)$	$2 + (-6) = -4$
4	$\bold{(-2) \cdot 6}$	$\bold{(-2) + 6 = 4}$
5	$3 \cdot (-4)$
6	$(-3) \cdot 4$

We can see that #4 meets both requirements of being multiples of -12 and having the sum equal 4!

And so we represent this as the factored version

$$\begin{split} (x + (-2))(x + 6) &= (x -2)(x + 6) \\ &= x^2 + 6x + (-4x) + (-12) \\ &= x^2 + 4x -12 \\ \end{split}$$

Medium

But what if we had the coefficient not 1 and instead 3:

$$3x^2 + 12x - 36$$

We would first factor out the a coefficient 3 and then we would have to extract multiples of 3 from b and c:

$$3(x^2 + 4x - 12$$

And we’re left with our result from the last quadratic we did which would be represented as

$$3(x - 2)(x + 6)$$

Split The Middle

$$3x^2 + 10x - 8$$

Immediately, you notice we cannot factor our the a coefficient because b = 10 doesn’t have multiples of 3 and neither does c = -8.

So wtf do we do here?

There’s a really cool technique NancyPi spoke about here, but I’ll try to explain it in my own words.

It’s quite similar to the strategy we had before it’s just multiplying factors of a * c and requiring the additive sum to be b instead of multiplying factors of c and additive sum being b.

The intuition behind it is that 10x can be recreated w/ 2 numbers, e.g., 2x + 8x = 10x while maintaining the multiplicitive result of a*c.

So we solve for

#	Multiples of a * c	Additive Sum = b
1	$1 \cdot 24$	$1 + -24 = -23$
2	$2 \cdot -12$	$2 + -12 = -10$
3	$-2 \cdot 12$	$-2 + 12 = 10$

So we have -2 and 12.

Then next part is to divide both of them by our a coefficient to create $\dfrac{-2}{3}$ and $\dfrac{12}{3}$ and since we can simplify the latter our final result will be:

$$\dfrac{-2}{3}$$ and $$\dfrac{4}{1}$$

And then we create our quadratic solution by using the denominator * x + numerator, creating:

$$(3x + (-2))(1x + 4) = (3x - 2)(x + 4)$$

Cannot Factor

There will come to a time where you will not be able to factor a quadratic. For example,

$$x^2 - 16x + 51$$

#	Multiples of a * c	Additive Sum = b
1	$1 \cdot 51$	$1 + -24 = -23$
2	$-1 \cdot 51$	$2 + -12 = -10$
3	$3 \cdot -17$	$-2 + 12 = 10$
3	$-3 \cdot 17$	$-2 + 12 = 10$

There are no solutions! And that’s kind of it…

---

No Constant

What happens if we don’t have a constant? Then we need to solve for each side of the multiplcation happening.

$$\begin{split} 4w^2 + 3w &= 0 \\ w(4w + 3) &= 0 \\ \\ \dfrac{w(\cancel{4w + 3})}{\cancel{\color{red}{4w + 3}}} &= \dfrac{0}{4w+3} \\[1em] w &= 0 \\ \\ \dfrac{\cancel{w}(4w + 3)}{\cancel{\color{red}{w}}} &= \dfrac{0}{w} \\[1em] 4w + 3 &= 0 \\ 4w &= -3 \\[1em] \dfrac{\cancel{4}w}{\cancel{\color{red}{4}}} &= \dfrac{-3}{4} \\[1em] w &= -\dfrac{3}{4} \\[1em] \end{split}$$

---

Completeing the Square

Standard

$$x^2 + 6x - 7 = 0$$

The first step is to move the constant onto the right side

$$x^2 + 6x = 7$$

Then we need to add the result of $\left( \dfrac{b}{2} \right)^2$ and add it to both sides

$$\begin{split} x^2 + 6x + \left( \dfrac{6}{2} \right)^2 &= 7 + \left( \dfrac{6}{2} \right)^2 \\[1em] x^2 + 6x + 9 &= 7 + 9 \\ (x + 3)^2 &= 16 \\ \end{split}$$

Why do we do this though? So we can have a perfect square:

$$(x + n)^2 = y$$

And we can solve for the xs by square rooting both sides

$$\sqrt{(x + 3)^2} = \pm\sqrt{16}$$

Why is there a plus-minus? Whenever we square root a constant we get a positive and a negative version (because a negative squared is a positive too!).

And so our result becomes

$$\begin{split} x + 3 &= \pm \sqrt{16} \\ &= \pm 4 \\ \end{split}$$

Then we solve for 2 equations, one for the positive and negative, as so:

For the positive,

$$\begin{split} x + 3 &= 4 \\ x &= 4 - 3 \\ x &= 1 \\ \end{split}$$

And the negative,

$$\begin{split} x + 3 &= -4 \\ x &= -4 - 3 \\ &= -7 \\ \end{split}$$

And we get our two solutions $x = 1$ and $x= -7$.

1 < a Coefficient

Lets say we have

$$2x^2 - 10x - 3 = 0$$

Our first step is the same by moving the 3 to the other side

$$2x^2 - 10x = 3$$

Next we want to get rid of that pesky a coefficient, which we do by dividing everything by a

$$\begin{split} \dfrac{2x^2}{2} \dfrac{- 10x}{2} &= \dfrac{3}{2} \\[1em] x^2 -5x &= \dfrac{3}{2} \\[1em] \end{split}$$

Now we want to add a new c to the left side of the equation and we must do the same to the right to make them equal.

And as we’ve done before this magic number is

$$\left(\dfrac{b}{2} \right)^2$$

Which in our case would be

$$\begin{split} \left( \dfrac{-5}{2} \right )^2 &= \dfrac{-5^2}{2^2} \\[1em] &= \dfrac{25}{4} \\ \end{split}$$

This, again, is the term that enables us to create a perfect square.

$$\begin{split} \left( \dfrac{-5}{2} \right )^2 &= \dfrac{-5^2}{2^2} \\[1em] &= \dfrac{25}{4} \\ \end{split}$$

And to get to our x solutions we

$$\begin{split} x^2 -5x + \dfrac{25}{4} &= \dfrac{3}{2} + \dfrac{25}{4} \\[1em] &= \dfrac{6}{4} + \dfrac{25}{4} \\[1em] &= \dfrac{31}{4} \\[1em] \left(x + \dfrac{-5}{2} \right)^2 &= \dfrac{31}{4} \\[1em] \sqrt{ \left(x + \dfrac{-5}{2} \right)^2} &= \pm \sqrt{\dfrac{31}{4}} \\[1em] x - \dfrac{5}{2} &= \pm \dfrac{\sqrt{31}}{\sqrt{4}} \\[1em] x &= \dfrac{5}{2} + \dfrac{\pm \sqrt{31}}{2} \\[1em] &= \dfrac{5 \pm \sqrt{31}}{2} \\[1em] \end{split}$$

Negative a Coefficient

$$-x^2 -6x + 7 = 0$$

Holy shit, a negative a coefficinet! Wtf will we ever do?!

Don’t worry, anon. The first still is always to move the c coefficient to the other side (oh that poor c).

$$-x^2 -6x = -7$$

We don’t want our a coefficient to be negative so we divide every term by -1 to flip the negative into a positive :)

\start{split} \dfrac{-x^2}{-1} \dfrac{-6x}{-1} &= \dfrac{-7}{-1} \\ x^2 + 6x &= 7 \\ \end{split}

Now that we got that frown upside down we just continue on our day. The left side is however lonely so we’re gonna need to give them a new fren, $\left(\drac{6}{2} \right)^2 = 9$. And we give the right side the same fren otherwise they’ll scream “INEQUALITY” and cause a riot.

\start{split} x^2 + 6x + 9 &= 7 + 9 \\ &= 16 \end{split}

And we’re back at the same answer as the solution we found in #Standard.

---

---

Vertex Form

Resources

• How to Solve By Completing the Square (NancyPi)