---

27/04 - College Algebra Prerequisities, Part 1

“The laws of nature are written in the language of mathematics.” - Galileo

Intro

Before starting anything:

1. A term can be a number, variable or product of numbers and variables, separates by plus or minus signs, e.g. $3x^2 + 5x + 2$ has 3 terms.
2. An expression is a combination of terms, which includes numbers, variables (letters that represent numbers), and arithmetic operations like addition, subtraction, multiplication, and division, e.g. $3x^2 + 5x + 2$ is an expression.
3. A product is the result of multiplication.
4. The quotient is the result of division.
5. A factor is a number or algebraic expression that divides another number or expression evenly.

For the retards, like myself, lets start with a quotient: the number returned from division, e.g. 15 is the quotient in $\dfrac{45}{3} = 15$.

What if we wanted to find the multiplicative inverse, aka the reciprocal? By swapping the numerator and denominator — since we know the answer is 15 aka $\dfrac{15}{1}$, $\dfrac{1}{15}$

A product, on the otherhand, is the number or expression resulting from the multiplication of two or more numbers or expressions, e.g. $10x^2 + 15x = 5x(2x + 3)$ where $5x(2x + 3)$ is the equivalent expression that is a product! This example contained factoring a polynomial (more on these later), which means finding an equivalent expression that is a product.

Sets

A set is a collection of objects that can be determined by $\{\}$, e.g. the roster method looks like $\{1, 2, 3, ...\}$.

Then we can move onto the intersection of sets. These are elements found in both sets, e.g. in $A=\{1,2,3\}$ and $B=\{3,4,5\}$ we see 3 is the common real number. We can say this as $A \cap B = \{3\}$. Think of this as a bridge where the number crosses from one side to the other!

Next, there is the use of the union $A \cup B$. Can you guess what this is? It’s the set of elements that are members of set $A$ or $B$ e.g. $\{1,2,3\} \cup \{3,4,5\} = \{1,2,3,4,5\}$! Think of this as a cup where we want one of each number flavour. We don’t want to overdose on number flavours so we add only one of each.

Real Number ($\Reals$)

Real numbers ($\Reals$) are, what I consider as, the letters of English alphabet. If we don’t know what letters there are how can we form words (the analogy for expressions and formulas)?

Subsets

There are subsets, think of as architypes in a game, that have different properties — try noticing the pattern between them as you go down.

Make a name for the new anime homie that assassinates his trbie, n’wiri (to remember the order: N, W, I, R, I)!

1. Natural numbers: nums we use for counting $\{1,2,3,...\}$
2. Whole numbers: natural numbers w/ 0, bc it felt lonely $\{0,1,2,3,...\}$
3. Integers: whole numbers that also went backwards $\{-3,-2,-1,0,1,2,3,...\}$
4. Rational numbers: rational numbers that can be expressed as the quotant (divide result) of 2 integers $\{-17 = \dfrac{-17}{1}, -3, 0, 2, 3, \dfrac{-2}{3} = -0.6666\}$
5. Irational numbers: all numbers where the decimals are neither terminating or repeating, so not quotient of integers $\{ \sqrt{2} \approx 1.414214, \pi \approx 3.142, -\dfrac{\pi}{2} \approx -1.571\}$

Everything is a rational number, aside from irrational numbers (duh).

Real Number Properties

The properties of real numbers are what we can do with said letters. What are the rules of the game so we can perform? These are super important to know. Without these you cannot go on to modify expressions, move terms around and solve equations — mastering these helps with calculus hardcore (from my experience).

1. Commutative: Changing the order doesn’t affect the sum; think as going to the store back and forth — the destination should be the same.
   • $13 + 7 = 7 + 13$
   • $\sqrt{2} \cdot \sqrt{5} = \sqrt{5} \cdot \sqrt{2}$
2. Associative: Changing grouping doesn’t affect the product; think as if i give you a pistol and you gave me an ak we can still shoot each other (lmao).
   • $-2(3x) = (-2 \cdot 3)x = -6x$
3. Distributive: Multiplying the outside var by the inner parentheses member(s); we’d use this to factor the like terms to make it simpler.
   • $a(b+c) = a \cdot b + a \cdot c$
   • $-3(4x - 2y +6) = -3 \cdot 4x - (-3) \cdot 2y - 3 \cdot 6$
4. Inverse: The inverse gives the same identity; we use this to simplify negative expressions.
   • Additive Inverse: $a + (-a) = 0$ and $(-a) + a = 0$
   • Multiplicitive Inverse: $a \cdot \dfrac{1}{a} = 1, \not = 0$ and $\dfrac{1}{a} \cdot a = 1, \not = 0$
5. Identity: Removing either 0 or 1 bc it doesn’t change anything; think of getting rid of your ex.
   • Additive Identity: $a + 0 = a$
   • Multiplicitive Identity: $a * 1 = a$

Absolute Value

The absolute value $|a|$ really means how far away are we from 0? If -3 is the answer then $|a| = 3$, for 3 it’s the exact same!

---

28/04 - College Algebra Prerequisities, Part 2

Exponents

Exponential notation looks like $b^n$, where $b$ is the base and $n$ is the exponent. For example, $b^3 \cdot b^2 = (b \cdot b \cdot b)(b \cdot b) = b^7$

There are a few rules we must understand, so we can modify expressions at will:

Product Rule

The product is the result of multiplying!

$$b^m \cdot b^n = b^{m+n}$$

For example, lets use this expression

$$(5x^2)(3x^4 - 6x^3 + 5x - 8)$$

When using the distributive property w/ $(5x^2)$ to $(3x^4)$ you should see think of it as

$$5 \cdot 3 = 15$$

And, with our exponents,

$$x^2 \cdot x^4 = x^{2+4} = x^6$$

BECAUSE

$$x^2 \cdot x^4 = x \cdot x \cdot x \cdot x \cdot x \cdot x = x^6$$

Then the final version is

$$= 15x^6$$

Then you can distribute and simplify the rest :)

Quotient Rule

The quotient is the output after dividing!

$$\dfrac{b^m}{b^n} = b^{m-n}, b \not = 0$$

If we have

$$\dfrac{b^5}{b^3}$$

Then we can think of it as

$$\dfrac{b \cdot b \cdot b \cdot b \cdot b }{b \cdot b \cdot b}$$

And we can cancel out like terms

$$\dfrac{\cancel{b \cdot b \cdot b} \cdot b \cdot b }{\cancel{b \cdot b \cdot b}}$$

To be left with

$$b \cdot b = b^2$$

Negative Exponent Rule

Typically in algebra we want the exponent to be positive and so we use this rule to get it to that state.

$$b^{-n} = \dfrac{b^{-n}}{1} = \dfrac{1}{b^n}$$

For example,

$$\dfrac{x^4}{x^7}$$

When we 4 - 7 we get -3 so

$$\dfrac{x^4}{x^7} = \dfrac{x^{-3}}{1}$$

But when when visually seeing the exponents before this negative exponent calculation

$$\dfrac{x^4}{x^7} = \dfrac{x \cdot x \cdot x \cdot x}{x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x}$$

Then when we cancel the like terms

$$= \dfrac{\cancel{x \cdot x \cdot x \cdot x}}{\cancel{x \cdot x \cdot x \cdot x} \cdot x \cdot x \cdot x}$$

We’re left with

$$= \dfrac{1}{x \cdot x \cdot x} = \dfrac{1}{x^3}$$

So that must mean that for any negative exponent on top we can inverse it and remove the subtraction operator applied to it!

$$\dfrac{x^4}{x^7} = \dfrac{x^{-3}}{1} = \dfrac{1}{x^3}$$

Zero-Exponent Rule

When the exponent is 0 then the result is 1!

To create the mental model, think that we have

$$\dfrac{b^2}{b^2} = \dfrac{\cancel{b \cdot b}}{\cancel{b \cdot b}} = b^{2-2} = b^0 = 1$$

What if we had

$$-3(7xy^6)^0)$$

Then everything in the parentheses will equate to 1, therefore

$$-3 \cdot 1 = -3$$

Power Rule

$$(b^m)^n = b^{mn}$$

E.g.

$$(2^2)^3 = (2^2) \cdot (2^2) \cdot (2^2) = 2^{2+2+2}$$

Products To Powers

Think of this as distributing the power to everything contained in the parentheses as a standalone.

$$(ab)^n = a^nb^n$$

E.g.

$$(3x)^2 = 3^2x^2$$

Quotients To Powers

Same as the products to power, except with rationals.

$$\left(\dfrac{a}{b}\right)^2 = \dfrac{a^2}{b^2}$$

---

I want to reiterate the concepts we just saw with this example, it will build your intuition ALOT more surprisingly,

$$\dfrac{5x^{-2}}{y^{-3}} \cdot \dfrac{8x^4}{y^{-5}}$$

I know what you’re thinking, “how the fuck am I going to solve this?!”

Remember, from the negative exponent rule, that we can inverse a variable if we also do the same for the exponent’s operator. Therefore, lets get rid of the negative exponents

$$= \dfrac{5y^3}{x^2} \cdot \dfrac{8x^4y^{5}}{1}$$

Lets get the product

$$= \dfrac{5y^{3+5}x^4}{x^2}$$

And remember the quotient rule for the xs

$$= \dfrac{5y^{3+5} \cdot x \cdot x \cdot \cancel{x \cdot x}}{\cancel{x \cdot x}}$$

Aka

$$= 5y^{8} x^2$$

---

Lets take it a step further and try this one,

$$\dfrac{24xy}{27x^{-2}} \div \dfrac{36x^2y^{-3}}{45xy^4}$$

There is the concept called [keep, change, flip] when dealing with rationals and multiplication/division. Essentially we keep one side of the expression, change the operator to the opposite (div to mul, or reverse) and flip the other side’s numerator and denominator. So lets do it here,

$$\dfrac{24xy}{27x^{-2}} \cdot \dfrac{45xy^4}{36x^2y^{-3}}$$

Now we can

$$\dfrac{6 \cdot 4 xy \cdot x^2}{9 \cdot 3} \cdot \dfrac{9 \cdot 5 x y^4 \cdot y^3}{6 \cdot 6 x^2}$$

Now we can look at it like this

$$\cancel{\dfrac{6}{6} \cdot \dfrac{9}{9} \cdot \dfrac{x^2}{x^2}} \cdot \dfrac{4xy}{3} \cdot \dfrac{5xy^7}{6}$$

Then simplifying further

$$= \dfrac{\cancel{2} \cdot 2 \cdot 5 x^2 y^8}{3 \cdot 3 \cdot \cancel{2}}$$ $$= \dfrac{10 x^2 y^8}{9}$$

---

What about for

$$\dfrac{x + 2}{5} = \dfrac{7}{8}$$

We can cross multiple the 5 * 7 and 8 distribute the x + 2

$$35 = 8x + 16$$

Remove 16 from both sides

$$19 = 8x$$ $$\dfrac{19}{8} = 2\dfrac{3}{8} = x$$

---

Radicals

Lets disect what a square root (sqrt) w/ the radical expression $\sqrt[n]{a} = b$

• $n$ is the radical index. If n is: odd then b, even then |b|.
• $\sqrt{}$ is the radical
• $a$ is the radicand, e.g. $\sqrt{4} = 2$ as $2^2 = 4$, where 4 is the principal sqrt.

Think of it as radi, [cal, and, index].

The principal nth root of a real number a $\sqrt[n]{a} = b$ means that $b^{n} = a$

Radical Factorisation

The perfect square is when a root’ed number returns an integer. If we have $\sqrt{36} = 6$, would be 6, bc multiplying itself (6^2), “perfectly” fits into 36.

If there is no perfect square, there will be factors of it. A factor is a number or expression that can be multiplied by another factor to get a product.

There is the greatest sqrt factor, referring to the largest perfect square that divides the number evenly, e.g. $\sqrt{50x} = \sqrt{{25 \cdot 2x}}$ since $25$ can be factored further we get $25 = 4 \cdot 5 \therefore \sqrt{{25 \cdot 2x}} = 4\cdot5\sqrt{2x} = 20\sqrt{2x}$

Another example is $\sqrt{500} = \sqrt{25 \cdot 20} = \sqrt{25} \sqrt{20} = 5 \sqrt{20}$. Since 20 contains a perfect square factor, 4, we need to simplify futher: $5 \sqrt{20} = 5 \sqrt{4 \cdot 5} = 5 \sqrt{4} \sqrt{5} = (5 \cdot 2) \sqrt{5} = 10\sqrt{5}$.

The aim is to get the lowest numbers to form the original number to make the expression less complex, e.g. for 36 we’d get $18 \cdot 2$ but we can go futher and do $9 \cdot 2$, then to get 36 we have the lowest factorisation w/ $3^2 \cdot 2^2 = 36$

Combining Radicals

Now with out new-found knowledge we can fight the mini boss battle: $4 \sqrt{50x} - 6\sqrt{32x}$

$$4 \sqrt{50x} - 6\sqrt{32x} = (4 \cdot x) \sqrt{5} \sqrt{2}$$

Radical Expression Rules

1. Product: The sqrt of a product is the product of sqrts, $\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}$
2. Quotient: If a (nominator) and b (the denominator) are nonnegative real numbers and b != 0, then: $\sqrt{\dfrac{a}{b}} = \dfrac{\sqrt{a}}{\sqrt{b}}$. The sqrt of a quotient is the quotient of the sqrts.

Add + Sub Radicals

• Add: $4\sqrt{11} + 2\sqrt{11} = (4+2)\sqrt{11} = 6\sqrt{11}$
• Sub: $\sqrt{5x} - 7 \sqrt{5x} = 1\sqrt{5x} - 7 \sqrt{5x} = (1-7) \sqrt{5x} = -6\sqrt{5x}$

Rationalising Denominators

This concept is where things started to click for me. Essentially, any number divided by itself is 1, e.g. $\dfrac{\sqrt{3}}{\sqrt{3}} = 1$.

So, 2 approximations that look entirely different, e.g. $\dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}$, can mean the same thing.

1. let’s break this down $\dfrac{1}{\sqrt{3}}$

$$\\ = \dfrac{1}{\sqrt{3}} \cdot 1$$ $$\\ = \dfrac{1}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}}$$

2. here’s the fascinating part: $$\\ = \dfrac{\sqrt{3}}{\sqrt{9}}$$
3. simplyfiying further $$\\ = \dfrac{\sqrt{3}}{3}$$
4. therefore $$\\ \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}$$

Conjugates

Radical expressions that involve the sum and difference of the same two terms are called conjugates (joint together).

The general rule for multiplying conjugates is:

$$(\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b}) = (\sqrt{a})^2 - (\sqrt{b})^2 = a - b$$

Why is this? We apply the Distributive property into:

$$(\sqrt{a} \cdot \sqrt{b}) (\sqrt{a} - \sqrt{b}) = (\sqrt{a} \cdot \sqrt{a}) + (\sqrt{a} \cdot (-\sqrt{b})) + (\sqrt{b} \cdot \sqrt{a}) + ((-\sqrt{b}) \cdot \sqrt{b})$$

Make this more readable:

$$= a - (\sqrt{ab})+(\sqrt{ab})-b$$

The like terms cancel out:

$$= - (\sqrt{ab})+(\sqrt{ab})$$

Which leaves us with:

$$= a -b$$

Lets look at another example, $\dfrac{h}{{\sqrt{x+h}} - \sqrt{x}}$ then the conjugate of the denominator is $\sqrt{x + h} + \sqrt{x}$ (the opposite).

As an example, $\dfrac{7}{5 + \sqrt{3}}$

$$\\ = \dfrac{7}{5 + \sqrt{3}} \cdot \dfrac{5 - \sqrt{3}}{5 - \sqrt{3}}$$

Rember how this is =1. Now we convert the two denominators to $(\sqrt{a})^2 - (\sqrt{b})^2$

$$\\ = \dfrac{7(5 -\sqrt{3})}{5^2 - (\sqrt{3})^2}$$

Simplify the denominator

$$\\ = \dfrac{7(5 -\sqrt{3})}{25 - 3}$$

Rational Exponents

Lets take a look at two expressions: $(7^{\frac{1}{2}})^2 = 7^{\frac{1}{2} \cdot 2} = 7^1 = 7$ and $(\sqrt{7})^2 = \sqrt{7} \cdot \sqrt{7} = \sqrt{49} = 7$

From this we see that: $7^{\frac{1}{2}}$ means $\sqrt{7}$

And so we can make the definition, as long as n >= 2:

$$a^\frac{1}{n} = \sqrt[n]{a}$$

And, as long as a != 0,

$$a^{-\frac{1}{n}} = \dfrac{1}{a^{\frac{1}{n}}} = \dfrac{1}{\sqrt[3]{a}}$$

But what about rationals where the numeration > 1?

$$a^\frac{2}{3} = (a^\frac{1}{3})^2 = (a^2)^\frac{1}{3}$$

Thus,

$$a^\frac{2}{3} = (\sqrt[3]{a})^2 = \sqrt[3]{a^2}$$

And we take this further with a new definition,

$$a^{\frac{m}{n}} = (\sqrt[n]{a})^m = \sqrt[n]{a^m}$$

And if $a^{-\frac{m}{n}}$ is a nonzero real number, then

$$a^{-\frac{m}{n}} = \dfrac{1}{a^\frac{m}{n}}$$

Notice how from the previous definition, $a^\frac{1}{n} = \sqrt[n]{a}$, n is the denominator and the only thing that changed was the numerator m. The reason why () come into play in the latter is because adding the exponent of 1 to something doesn’t change anything! So really, the latter is the general definition of rational exponents!

Lets do an example:

$$\dfrac{32^\frac{5}{3}}{16x^\frac{3}{4}} = \left(\dfrac{32}{16}\right)\left(\dfrac{x^\frac{5}{3}}{x^\frac{3}{4}}\right)$$ $$= 2x^{\frac{5}{3} - \frac{3}{4}}$$

Now, if you’re mathematically illiterate like myself, we need to simplify this mofo right here. It’s a bit confusing but I’ve done the hard work for the tribe:

We begin by finding the common denominator w/ 3 and 4: 12, essentially the lowest number w/ both numbers — like factoring.

So for ${\dfrac{5}{3} - \dfrac{3}{4}}$ we’re really just multiplying the numerator 5 and denominator 3 by the opposite expression’s denominator 4:

$$\dfrac{5}{3} = \dfrac{5\cdot4}{3\cdot3} = \dfrac{20}{12}$$

And do for the other expression with the former,

$$\dfrac{3}{4} = \dfrac{3\cdot3}{4\cdot3} = \dfrac{9}{12}$$

Then we get

$$= \dfrac{20}{12} - \dfrac{9}{12} = \dfrac{20 - 9}{12}= 2x^{\frac{12}{11}}$$

We finally got through the core sht! Only [polynomials, factoring, trig] to go (fck me it takes ages to write about this stuff, but damn is it sticking).

---

02/05 - Polynomials!

Gm, welcome to learning about pole-pee-no-my-balls.

As always, lets learn the Vocabulary first, wtf are nomials:

• Monomial is a single term, $7x^3$
• Binomial: is 2 terms, $7x^3 + 2x^2$
• Trinomial: is 3 terms, $7x^3 + 2x^2 + 5$
• Polynomial: is anything beyond 3 terms, $7x^3 + 2x^2 + 5x + 69$

We describe polynomials w/ negatives w/ parentheses to be explicit (like a rap song)

$$7x^3 - 9x^2 + 13x - 6$$

As, $$7x^3 + (-9x^2) + 13x + (- 6)$$

I trip up a lot with the - bullshit so this is quite important to note: $-ax^n = (-ax^n)$.

The n represents the degree. We order polynomials in cronological order from left to right in terms of degrees. E.g. $7x^3$ will be ordered before $7x^2$. The degree of a polynomial is the greatest of the degress of all its terms.

Taking a look at an algebraic expression w/ a polynomial in x (expression of vars + coefficients combined using addition, subtraction and multiplication): $$a_{n}x^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1x + a_0$$

• The degree of the polynomial is $n$. This is important because it is the biggest rate of change.
• The leading coefficient (numerical or constant factor that multiplies a var) (the term w/ the highest exponent/power) is $a_n$
• The constant term is $a_0$

Polynomial Sub, Add, Mul

Subtracting polynomials by combining like terms (variables and their exponent powers are the same), e.g.

$$-9x^3 - 13x^3 = (-9 + 13)x^3 = 4x^3$$

We are using the the distributive property to factor out the common term, $x^3$

Adding polynomials: $5x^4 + 6x^4 = 11x^4$

However we cannot Simplify $5x^4 + 3x^2$ because there are no like terms!

Multiplying polynomials:

$$(5x^4)(6x^4)$$

Combining like terms,

$$= (5\cdot6)(x^4 \cdot x^4)$$ $$= 30x^{4+4} = 30x^8$$

But what would we do if there is no monomials? E.g,

$$(2x + 3) (x^2 + 4x + 5)$$

Well we would use the distributive property (our lord and saviour!):

Distributing 2x

$$2x(x^2 + 4x + 5) = 2x^3 + 8x^2 + 10x$$

Then distributing 3

$$3(x^2 + 4x + 5) = 3x^2 + 12x + 15$$

Then combining like terms

$$= 2x^3+ (3x^2 + 8x^2) + (10x + 12x) + 15$$

Simplifying

$$= 2x^3+ 11^2 + 22x + 15$$

Product Of Two Binomials

Once again, we use the distributive property to find the product of two binomials. For example,

$$(3x - 5) (4x + 5)$$ $$= 3x(4x) + 3x(5) + (-5(4x)) + (-5(5))$$ $$= 12x^2 + 15x + (-20x) + (-25)$$ $$= 12x^2 + -5x -25$$

Similar to multiplying conjugates, we find the Product of the Sum and Difference of Two Terms as follows: $$(A + B)(A - B) = A^2 - B^2$$ because the two terms cancel eachother out $$(B \cdot A) (A \cdot (- B)) = AB - AB = 0$$

Squaring & Cubing Binomials

$$(A + B)^3 = A^3 + 3A^2B + 3AB^2 + B^3$$

How do we break this down? Lets expand the exponents:

$$(A + B)^3 = (A + B) (A + B) (A + B)$$

Lets distribute the first 2:

$$(A + B) (A + B) = A^2 + AB + AB + B^2 = A^2 + 2AB + B^2$$

Now we distribute the third:

$$= (A^2 + 2AB + B^2) (A + B)$$ $$= (A^3 + 2A^2B + 2AB^2 + B^3)$$

---

03/05 - Factoring Polynomials

Factoring

Factoring a polynomial containing the sum of monomials means finding an expression that is a product:

$$10x^2 + 15x = 5x(2x+3)$$

The goal of factoring a polynomial is: to use one or more factoring techniques until each of the polynomial’s factors, except possibily for a monomial factor, is prime (a natural number, greater than 1, that is not the product of two smaller natural numbers) or irreducible, aka being factored completely.

The greatest common factor (GCF) is the largest positive integer that divides two or more integers without leaving a remainder.

$$18x^3 + 27^2$$

9 factors into 18 (9*2) and 27 (9*3),

$$= 9x^2(2x) + 9x^2(3)$$

What about for,

$$x^2 (x+3) + 5(x + 3)$$

We see that $(x + 3)$ is the common factor in both terms, so we can reverse the distributive property into:

$$(x + 3) (x^2 + 5)$$

Factoring By Grouping

Some polynomials only have 1 as the greatest common factor. But by grouping the terms together we can actually create the common factor.

For example, these terms have the common factor of 1,

$$x^3 + 4x^2 + 3x + 12$$

If we group them together then we may be able factor out something that is common

First, the common factor is $x^2$ with:

$$(x^3 + 4x^2) = x^2(x+4)$$

The second, with the common factor of $3$, becomes

$$(3x + 12) = 3(x + 4)$$

Combining them together we get

$$= x^2(x + 4) + 3(x + 4)$$

Notice the common factor again? It’s $(x + 4)$. We use this as one term then the other would be the remaining vars, $(x^2 + 3)$. Therefore,

$$= (x + 4)(x^2 + 3)$$

---

Lets do one that isn’t so intuitive

$$2x^2 + 3 - 2 = 0$$

Since there isn’t any factors that equate to -2 when multiplying them together and add up to 3 we multiply -2 by our coefficient 2 from $2x^2$ to create -4 for factoring.

Now we can factor 4 and -1 to create

$$2x^2 + 4x -1x - 2 = 0$$

Notice how the result doesn’t change!!

Now we can factor by grouping since there are 4 terms

$$2x(x + 2) - 1 (x + 2) = 0$$

Then we factor out x + 2

$$(x + 2)(2x - 1) = 0$$

And now we can solve the expression

$$x + 2 = 0$$ $$x = -2$$

and

$$2x - 1 = 0$$ $$2x = 1$$ $$x = \dfrac{1}{2}$$

Factoring Trinomials

Lets try factor a trinomial in two variables:

$$2x^2 -7xy + 3y^2$$

First we need to find the first 2 terms that create $2x^2$ when distributed

$$(2x + ..) (x + ..)$$

Then we need to figure out the remaining two terms that whose product is $3y^2$

$$(y)(3y) = (-y)(-3y)$$

Finally, we need to make sure the sum of the far left and right products is equal to $-7xy$

$$(2x + -y) (x + -3y)$$

Then we can verify but distributing it

$$= (2x \cdot x) + (2x \cdot -3y) + (-y \cdot x) + (-y \cdot -3y)$$

Simplify

$$= 2x^2 - 6xy - xy - 4y$$

And, we’re back where we started!

$$= 2x^2 - 7xy - 4y$$

Factoring Difference Of Two Squares

$$A^2 - B^2 = (A + B)(A - B)$$

For example,

$$81x^2 - 49$$ $$= \sqrt{81x^2} - \sqrt{49}$$ $$= (9x)^2 - 7^2$$ $$= (9x + 7)(9x - 7)$$

Repeated Factorisation

This is when we can factorise a term further after factorising the expression.

For example,

$$x^4 - 81$$ $$= \sqrt{x^4} - \sqrt{81}$$ $$= (x^2)^2 - 9^2$$

Difference of squares

$$= (x^2 + 9)(x^2 - 9)$$

Factoring further step

$$= (x^2 + 9)(x^2 - \sqrt{9})$$

Notice that we now have a square subtracting another square, $(x^2 - 3^2)$. We can factor further w/ the difference of two squares again ($A^2 - B^2 = (A + B)(A - B)$) only because it’s subtracting. We cannot do the same for $(x^2 + 9)$ because its adding, which is not the difference of two squares requirement, $A^2 - B^2$. If we were expand, we’d be doing the opposite of factoring.

$$= (x^2 + 9)(x^2 - 3^2)$$ $$= (x^2 + 9)(x + 3)(x - 3)$$

This took me a while to understand this, so don’t beat yourself up — I was seriously lost lmao. The main point is the subtraction enables the difference of two squares factorisation, whereas addition does not.

Factoring Perfect Square Trinomials

Before we start, a perfect square trinomial is a trinomial that can be factored into two identical binomial factors, e.g. $x^2 + 6x + 9 = (x+3)(x+3) = (x+3)^2$.

There are ways to factor a percect square trinomial. Notice how the first sign is reflected as the sign in the parentheses.

1. $A^2 + 2AB + B^2 = (A + B)^2$
2. $A^2 - 2AB + B^2 = (A - B)^2$

We identify a perfect square trinomial via:

1. The first and last terms being squares of monomials or integers
2. The middle term is twice the product of the expressions being squared in the first and last terms

E.g,

$$25x^2 - 60x + 36$$

Break down the terms w/ sqrts

$$= \sqrt{25x^2} - 60x + \sqrt{36}$$

Now we have the sqrt product

$$= (5x)^2 - 60x + 6^2$$

Verify the middle term is twice the product of the outer two

$$60x = 2(5x)(6)$$

It is, therefore

$$= (5x - 6)^2$$

Factoring the Sum and Difference of Two Cubes

Factoring the Sum of Two Cubes

$$A^3 + B^3 = (A + B)(A^2 - 2AB + B^2)$$

Factoring the Difference of Two Cubes

$$A^3 - B^3 = (A - B)(A^2 + 2AB + B^2)$$

Notice how the first parentheses uses the same sign as the 2nd term and then the 2nd parentheses use the opposite of the 2nd term’s sign.

For example,

$$64x^3 - 125$$ $$= \sqrt[3]{64} - \sqrt[3]{125} = (4x)^3 - 5^3$$ $$= \sqrt[3]{64} - \sqrt[3]{125} = 4^3 - 5^3$$ $$= (4 - 5)(4^2 + 2(4)(5) + 5^2)$$

Factoring Polynomial Strategy

Factoring is super important to grasp as it’s how we can simplify expressions drastically. And since polynomials are extremely common in mathematics we want to be well equiped with all tools at our disposal, which is why algebra is so god damn important — good luck doing anything beyond this if you don’t truly undersatnd algebra.

1. If there is a common factor, factor out the greatest common factor
2. Check how many terms there are then:
   1. 2 terms:
      • Difference of two squares: $A^2 - B^2 = (A + B)(A - B)$
      • Sum of two cubes: $A^3 + B^3 = (A + B)(A^2 - 2AB + B^2)$
      • Difference of two cubes: $A^3 - B^3 = (A - B)(A^2 A 2AB + B^2)$
   2. 3 terms: If perfect square trinomial use the following, otherwise trial and error:
      • $A^2 + 2AB + B^2 = (A + B)^2$
      • $A^2 - 2AB + B^2 = (A - B)^2$
   3. 4+ terms, try factoring by grouping
3. If more than 1 term in the factored polynomial can be further factored, go further until factored completely

Factoring Fractional Exponents

$$x(x + 1)^{-\frac{3}{4}} + (x+1)^{\frac{1}{4}}$$

We have the greatest common factor $(x + 1)^{-\frac{3}{4}}$. Express each term w/ the GCF

$$= (x + 1)^{-\frac{3}{4}}x + (x + 1)^{-\frac{3}{4}}(x+1)$$

Factor out GCF

$$= (x + 1)^{-\frac{3}{4}} [x + (x + 1)] = (x + 1)^{-\frac{3}{4}} [2x + 1]$$

Then we use the previously discussed negative quotient rule, $b^{-n} = \dfrac{1}{b^n}$. Remember we get rid of the negative sign on the rational exponent and switch from multiplying to dividing!

$$= \dfrac{2x + 1}{(x + 1)^{\frac{3}{4}}}$$

---

05/05 - Rational expressions

Speaking of rationals, we’re almost at the end of our retardo-prep for algebra! Only a fraction of the way left (lmao, kill me)!

Wtf is a rational expression? The quotient (product of division) of two polynomials, e.g. $\dfrac{x}{x^2 - 1}$

Since rational expressions are division and division by zero is undefined we must establish the domain, e.g. for $\dfrac{x}{x - 2}$ our domain would be $x \not = 2$ otherwise the rational could be 0, and everyhing will crash and burn. And so our full expression is $$\dfrac{x}{x - 2}, x \not = 2$$

Simplifying Rational Expressions

A rational express is only simplified if its numerator and denominator have no common factors other than 1 or -1

1. Factor the numerator and the denominator completely
2. Divide both the numerator and the denominator by any commmon factors

For example,

$$\dfrac{x^2 + 6x + 5}{x^2 - 25}$$

Look for how we can factor further — sqrt into perfect square

$$= \dfrac{x^2 + 6x + 5}{x^2 - \sqrt{25}}$$

Denominator difference of two squares

$$= \dfrac{x^2 + 6x + 5}{x^2 - 5^2}$$

Factor; reverse distribute

$$= \dfrac{x^2 + 6x + 5}{(x + 5)(x - 5)}$$

Turn quadratic numerator into binomial expression (we find 2 numbers that add up to the middle term 6x). We can actually cancel out like terms here, $(x + 5) = 1$, and make them both 1

$$= \dfrac{(x + 5)(x + 1)}{(x + 5)(x - 5)}$$

Since we canceled 5 out from the numerator and and the -5 from our simplified denominator (from 25), our domain is added to our expression

$$= \dfrac{(x + 1)}{(x - 5)}, x \not = \{-5, 5\}$$

Multiplying Rational Expressions

$$\dfrac{x-7}{x-1} \cdot \dfrac{x^2 - 1}{3x-21}$$

Difference of two squares and apply factor the common factor

$$= \dfrac{x-7}{x-1} \cdot \dfrac{(x + 1)(x - 1)}{3(x - 7)}$$

Notice how we have the same terms on both sides, $(x - 7)$ and $(x - 1)$, so we can cancel them out (bc it doesn’t change the final result)

$$= \dfrac{x + 1}{3}$$

Since The denominator has factors of x - 1 and x - 7 then domain is x != [1, 7]

$$= \dfrac{x + 1}{3}, x \not = 1, x \not = 7$$

Dividing Rational Expressions

$$\dfrac{x^2 - 2x - 8}{x^2 - 9} / \dfrac{x - 4}{x + 3}$$

Swap the sign to multiply and swap numerator and denominator

$$= \dfrac{x^2 - 2x - 8}{x^2 - 3^2} \cdot \dfrac{x + 3}{x - 4}$$

Difference of two squares + factoring a quadratic

$$= \dfrac{(x - 4)(x + 2)}{(x + 3)(x - 3)} \cdot \dfrac{x + 3}{x - 4}$$

Common terms in both rationals; we can cancel them and they get removed from our domain (x != [-3, 3, 4]). Remember we can’t have the rational = 0.

$$= \dfrac{x + 2}{x - 3}, x \not = \{-3, 3, 4\}$$

Add & Subtract Rational Expressions

Rational numbers that have no common factors in their denominators can be added or subtracted w/ one of the following properties:

Addition

$$\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ab + bc}{bd}, b \not = \{0, d\}$$

Subtraction

$$\dfrac{a}{b} - \dfrac{c}{d} = \dfrac{ab - bc}{bd}, b \not = \{0, d\}$$

Notice how they cross divide for the numerators and the denominators they multiply themselves.

Examples

Example w/ the same denominator

$$\dfrac{5x + 1}{x^2 - 9} - \dfrac{4x - 2}{x^2 - 9}$$

Combine the terms into a single expression bc of the same denominator

$$= \dfrac{5x + 1 - (4x -2)}{x^2 - 9}$$

Remove the parentheses and change the sign of each term within

$$= \dfrac{5x + 1 - 4x + 2}{x^2 - 9}$$

We can factor 9 into a perfect square w/ sqrt

$$= \dfrac{5x + 1 - 4x + 2}{x^2 - 3^2}$$

difference of two squares!

$$= \dfrac{x + 3}{(x + 3)(x - 3)}$$

Remove like terms + express the domain

$$= \dfrac{1}{x - 3}, x \not = \{-3, 3\}$$

Simple enough, right?

---

Lets up the ante and try something that will probably be spotted in the wird more often. One w/ no common factors in the denominators?

$$\dfrac{x + 2}{2x-3} - \dfrac{4}{x+3}$$

Cross multiply numerators and multiply both denominators

$$= \dfrac{(x+2)(x+3) - (2x - 3)4}{(2x-3)(x+3)}$$

We don’t open the parentheses bc that was the variable we were given with

$$= \dfrac{x^2 + 5x + 6 - (8x - 12)}{(2x-3)(x+3)}$$

We can remove the parentheses and change sign of each term within

$$= \dfrac{x^2 + 5x + 6 - 8x + 12}{(2x-3)(x+3)}$$

Simplify and specify domain,

1. $2x−3=0$ leads to $x = \dfrac{3}{2}​$

   because $2x − 3 = 0$ equals $2x = 3$ then further $x = \dfrac{3}{2}$

2. $x+3=0$ leads to $x= −3x = −3$

$$= \dfrac{x^2 - 3x + 18}{(2x-3)(x+3)}, x \not = \{\dfrac{3}{2}, -3\}$$

---

Least Common Denominator

It is the smallest positive integer that is divisible by all the denominators in a set of fractions.

Lets do an example,

$$\dfrac{x + 3}{x^2 + x - 2} + \dfrac{2}{x^2 - 1}$$

First, we need to find the least common denominator by factoring the denominators

1. $x^2 + x - 2 = (x + 2)(x - 1)$ because $x^2 + x + 2 = (x - 2)(x + 1)$
2. $x^2 - 1 = (x + 1)(x - 1)$

Therefore,

$$= \dfrac{x + 3}{(x + 2)(x - 1)} + \dfrac{2}{(x + 1)(x - 1)}$$

We can see the only factor not in the first denominator is $(x + 1)$ therefore the least common denominator is $(x + 2)(x - 1)(x + 1)$

So we add it onto both,

$$= \dfrac{x + 3}{(x + 2)(x - 1)} \cdot \dfrac{x + 1}{x + 1} + \dfrac{2}{(x + 1)(x - 1)} \cdot \dfrac{x + 2}{x + 2}$$

Rearrange the right denominator to match the left

$$= \dfrac{(x + 3)(x + 1)}{(x + 2)(x - 1)(x + 1)} + \dfrac{2(x + 2)}{(x + 2)(x - 1)(x + 1)}$$

Keep in mind this isn’t actually changing the outcome, only the appearance. But we can start to sum these up.

$$= \dfrac{(x + 3)(x + 1) + 2(x + 2) }{(x + 2)(x - 1)(x + 1)}$$

Then simplify it

$$= \dfrac{x^2 + 4x + 3 + 2x + 4}{(x + 2)(x - 1)(x + 1)}$$

Combine like terms + establish the domain

$$= \dfrac{x^2 + 6x + 7}{(x + 2)(x - 1)(x + 1)}, x \not = \{-2, 1, -1\}$$

---

Complex Rational Expressions

Aka complex fractions have numerators or denominators containing one or more rational expressions, e.g. $\dfrac{1 + \dfrac{1}{x}}{1 - \dfrac{1}{x}}$ or $\dfrac{\dfrac{1}{x + h} - \dfrac{1}{x}}{h}$

For example, let’s simplify

$$\dfrac{1 + \dfrac{1}{x}}{1 - \dfrac{1}{x}}$$

We start by getting the lowest common denominator $1(x)$

$$= \dfrac{\dfrac{1}{1} + \dfrac{1}{x}}{\dfrac{1}{1} - \dfrac{1}{x}}$$

The goal here is to have the denominators match to make everything easier. So whatever we don’t have for one denominator we want to add the opposite one. Remember anything you do to the denominator you do to the numerator.

In this case the LCD $x \cdot 1$ is applied by adding $x$ to the left fraction, $1$ to the right fraction (remains the same).

$$= \dfrac{\dfrac{1 \cdot x}{1 \cdot x} + \dfrac{1 \cdot 1}{x \cdot 1}}{\dfrac{1 \cdot x}{1 \cdot x} - \dfrac{1 \cdot 1}{x \cdot 1}}$$

Do the calculation

$$= \dfrac{\dfrac{x}{x} + \dfrac{1}{x}}{\dfrac{x}{x} - \dfrac{1}{x}}$$

The denominators are now the exact same we can merge the fractions together

$$= \dfrac{\dfrac{x + 1}{x}}{\dfrac{x - 1}{x}}$$

Invert and multiply; Division by a fraction is equivalent to multiplication by its reciprocal.

The reciprocal of a fraction is created by swapping its numerator and denominator.

For example, the reciprocal of $\dfrac{a}{b}$ is $\dfrac{b}{a}$, provided that a and b are non-zero.

$$= \dfrac{x + 1}{x} \cdot \dfrac{x}{x - 1}$$

Remove like terms that cross, x.

Why?

Beause multiplication is commutative, the ordering doesn’t matter!

So, $\dfrac{x + 1}{x} \cdot \dfrac{x}{x - 1}$ can be represented as $\dfrac{x + 1}{x - 1} \cdot \dfrac{x}{x}$ which is the same as $\dfrac{x + 1}{x - 1} \cdot 1$

And we finally get

$$= \dfrac{x + 1}{x - 1}$$

---

I want to show another example that I personally struggled for 2 weeks on, causing me go down the rabbit hole of why I’m so stupid.

$$\dfrac{\dfrac{1}{x + h} - \dfrac{1}{x}}{h}$$

The first thing we should do is forget about the $\dfrac{}{h}$ so we can focus on the numerator, $$\dfrac{1}{x + h} - \dfrac{1}{x}$$

Next we need make the denominators the same.

We do this by asking ourselves “what is the least common denominator?” (the smallest number that can be used as the denominator for all fractions in a set). What would make the denominators the same?

If we multiply the left by x and the right by x + h we get $x(x+h)$

$$\dfrac{(1)x}{(x + h)x} = \dfrac{x}{x(x+h)}$$

and the right side,

$$\dfrac{(1) x+h}{(x) x+h} = \dfrac{x+h}{x(x+h)}$$

now we can merge the two, remembering the subtraction operator

$$= \dfrac{x}{x(x+h)} - \dfrac{x+h}{x(x+h)}$$

After merging

$$= \dfrac{x - (x+h)}{x(x+h)}$$

Here’s a small detail but -(x+h) actually means -1(x+h), and so

$$= \dfrac{x - 1(x+h)}{x(x+h)}$$

We can apply the distributive property

$$= \dfrac{x - x - h}{x(x+h)}$$

Notice the xs cancel out in the numerator

$$= \dfrac{0 - h}{x(x+h)} = \dfrac{- h}{x(x+h)}$$

Now we can add the $\dfrac{}{h}$

$$= \dfrac{\dfrac{- h}{x(x+h)}}{h}$$

We can reverse the division of h into multiplication into it’s numerator $x(x+h)$

$$= \dfrac{- h}{hx(x+h)}$$

We can cancel the hs out bc they’re both products w/ common factors

$$= \dfrac{-1}{1x(x+h)}$$

And just to make it cleaner

$$= -\dfrac{1}{x(x+h)}$$

Jeeeeez, what a ride! I hope you finally understand how this works :) This shit took me 2 god damn weeks to ravel my head around — went into how factorisation, fraction cancelation and simplificaiton.

---

14/05 — Simplifying

Factoring

Factoring is the process of changing a sum to a product.

For example, lets start w/ the 4 term sum $$ax + ay + bx + by$$

We factor it into a 2 term sum, bc we still have the addition operator

$$= a(x + y) + b(x + y)$$

Then we complete the factorisation by turning it into a product, distinguished by the multiplication operator.

$$=(x + y)(a + b)$$

Reducing Fractions

$$\dfrac{x(x - 2) - 15}{(x-2)(x + 3)}$$

We can only reduce if both numerator and denominator are products. You cannot reduce until they’re products.

The subtraction operation makes the numerator a sum, the denominator is a product. We cannot cancel out the $x-2$ bc one is a sum and the other is a product, we need the common elements to be factors. So how do we convert the numerator into a product?

First we distribute the x

$$= \dfrac{x^2 - 2x - 15}{(x-2)(x + 3)}$$

Then factor the trinomial in the numerator, creating a product in the numerator

$$= \dfrac{(x - 5)(x + 3)}{(x-2)(x + 3)}$$

Cancel the common factor, x + 3, bc it equals to one $\dfrac{x+3}{x+3}$

$$= \dfrac{x - 5}{x-2}$$

Canceling

I personally struggled so much with simplifying. It was not intuitive to me at all. But let me break it down for you.

The entire concept of simplifying is to keep the extression output the same while making the expression itself easier to read.

E.g. going from $\dfrac{12}{15}$ to $\dfrac{4}{5}$ is the same as the factorisation via $\dfrac{4 \cdot 3}{5 \cdot 3}$ which can be split into a product of two fractions $\dfrac{4}{5} \cdot \dfrac{3}{3}$

You’ll notice the common factors are split into a single fraction so they can be divided to produce a 1, which doesn’t change the other fraction, $\dfrac{3}{3} = 1$ and so $\dfrac{4}{5} \cdot 1 = \dfrac{4}{5}$.

---

Lets try a one with variables $\dfrac{x^2 - x - 6}{x^2 - 9}$.

Your intution may be to cancel the $x^2$ because they’re exactly the same BUT HOLD ON! When we go through the process of splitting them off $\dfrac{x^2}{x^2} \cdot \dfrac{- x - 6}{- 9}$ it isn’t equal because they are not factors, we were never multiplying them to begin with in the expression.

If x = 2, $x^2 = 4$ then $4 - 2 - 6 = -4$, but with the splitting off we get $$4(-2-6) = 4(-8) = -32$$

What we actually have to do is factor the numerator and denominator to find common factors $$\dfrac{x^2 - x - 6}{x^2 - 9} = \dfrac{(x-3)(x+2)}{(x-3)(x+3)}$$

but we can cross out the ${(x-3)}$‘s since

$$= \dfrac{(x-3)(x+2)}{(x-3)(x+3)} = \dfrac{x-3}{x-3} \cdot \dfrac{x+2}{x+3} = 1 \cdot \dfrac{x+2}{x+3} = \dfrac{x+2}{x+3}$$

---

Another example that will trip you up is $\dfrac{x^2 - 3(x+6)}{(x-6)(x+6)}$ bc we cannot separate it into a product bc the numerator is a sum $$\not = \dfrac{x^2 - 3}{x - 6 } \cdot \dfrac{x + 6}{x + 6}$$

The denominator is functionally the same, however the numerator’s subtraction operator is the reason we cannot

$$x^2 - 3 (x + 6) \not = (x^2 - 3)(x + 6)$$

The incorrect simplifaction expression that would the wrong intuitive answer, $$= \dfrac{x^2 -3}{x - 6} \cdot \dfrac{x + 6}{x + 6} = \dfrac{(x^2 - 3) (x + 6)}{(x - 6)(x + 6)}$$

Where $x = 3$

$$\dfrac{(3^2 - 3)(3 + 6)}{(x - 6)(x + 6)} = \dfrac{(9 - 3)(3 + 6)}{(x - 6)(x + 6)}$$

Distribute

$$= \dfrac{(9\cdot 2) + (9 \cdot 6) + ((-3) \cdot 3) + ((-3) \cdot 6)}{(x - 6)(x + 6)}$$ $$= \dfrac{18 + 54 + (-9) + (-18)}{(x - 6)(x + 6)}$$ $$= \dfrac{45}{(x - 6)(x + 6)}$$

As for the correct simplifaction,

$$\dfrac{3^2 - 3 (3 + 6)}{(x - 6)(x + 6)}$$ $$= \dfrac{3^2 - 3 (9)}{(x - 6)(x + 6)}$$ $$= \dfrac{9 - 3 (9)}{(x - 6)(x + 6)}$$

We don’t calculate the 9 - 3 over only the -3 bc it’s not together in parentheses! The far left 9 remains but we multiply the 3 by the parentheses 9.

$$= \dfrac{9 - 27}{(x - 6)(x + 6)}$$ $$= \dfrac{−18}{(x - 6)(x + 6)}$$

---

Or if we weren’t using 3 as x,

$$\dfrac{x^2 - 3 (x + 6)}{(x-6)(x+6)}$$

We distribute

$$= \dfrac{x^2 - 3x - 18}{(x-6)(x+6)}$$

Then we factor the numerator’s trinomial, looking for 2 numbers that multiply to -18 and add up to -3.

$$= \dfrac{(x - 6)(x + 3)}{(x-6)(x+6)}$$

And now we have a common factor that we can cross out, $(x-6)$, because it can be split into the product of 2 fractions!

$$= \dfrac{x - 6}{x-6} \cdot \dfrac{x + 3}{x+6}$$ $$= 1 \cdot \dfrac{x + 3}{x+6}$$

---

Now lets do an extreme example including exponents!

$$\dfrac{8a^{10}b^{4}}{12a^8b^7}$$

First we factor the real numbers

$$= \dfrac{4 \cdot 2 a^{10}b^{4}}{4 \cdot 3 a^8b^7}$$

Then we can factor the a exponents. We split it up so the $a^8$ match for the cancelation later :)

$$= \dfrac{4 \cdot 2 a^8 a^2 b^{4}}{4 \cdot 3 a^8b^7}$$

And lastly we have the b exponents — do you notice anything, anon?

$$= \dfrac{4 \cdot 2 a^8 a^2 b^{4}}{4 \cdot 3 a^8 b^3 b^4}$$

To clean it up a bit more we can separate the product of fractions. Remember multiplication is commutative so it doesn’t matter what order you put the fractions in!

$$= \dfrac{4 a^8 b^4}{4 a^8 b^4} \cdot \dfrac{2 a^2}{3 b^3}$$

And they cancel bc it’s equal to 1 which is the same as having nothing.

$$= 1 \cdot \dfrac{2 a^2}{3 b^3}$$

---

Equations and Inequalities

There are 4 quadrants (quarters) on a rectangular coordinate system in order of [top right, top left, bot left, bot right]. The center point is the origin. Each point is an ordered pair in terms of (x, y). An intercept is when the graph passes through a point. There can be multiple intercepts!

A linear equation w/ a single var is: $ax + b = 0$ where a and b are real numbers and a != 0, e.g. $4x + 12 = 0$

Solving an equation in $x$ involves determining all values of $x$ that result in a true statement when substituted into the equaion.

If two or more equations have the same solution set they are called equivalent equations.

Solving Linear Equations

Let say we have the linear equation

$$2x + 3 = 17$$

Our aim is to isolate the x.

We can start off by subtracting the 3 from both sides to make it equal

$$2x + 3 - 3 = 17 - 3$$ $$2x = 14$$

Then we can reverse the multiplication of 2x into division, and then applying it to the other side too to preserve the equality, if we didn’t it would no longer be equal.

$$\dfrac{2x}{2} = \dfrac{14}{2}$$

This cancels out 2 so we have x on one side of the equation bc

$$\dfrac{2}{2} \cdot \dfrac{x}{1}$$ $$= 1 \cdot \dfrac{x}{1}$$

Reverse the multiplication

$$= \dfrac{x}{1} = x \cdot 1 = x$$

Then we get our isolated var

$$x = 7$$

---

What about one with fractions?

For example,

$$\dfrac{x + 2}{4} - \dfrac{x - 1}{3} = 2$$

Luckily we’ve got the fundamental algebra skills to deal with this.

Lets start by finding the smallest number that is divisible by 4 and 3 to get the least common denominator:

1. 3: [3, 6, 9, 12]
2. 4: [4, 8, 12, 16]

The LCD is 12 therefore we multiply both sides by 12

$$12\left(\dfrac{x + 2}{4} - \dfrac{x - 1}{3}\right) = 24$$

Use the distributive property,

$$12\left(\dfrac{x + 2}{4}\right) - 12\left(\dfrac{x - 1}{3}\right) = 24$$

Divide out the common factors in each multiplication on the left. 12 splits into 3 * 4 for the left side and the opposite for the right.

$$(3 \cdot \cancel{4})\left(\dfrac{x + 2}{\cancel{4}}\right) - (\cancel{3} \cdot 4)\left(\dfrac{x - 1}{\cancel{3}}\right) = 24$$ $$3\left(\dfrac{x + 2}{1}\right) - 4\left(\dfrac{x - 1}{1}\right) = 24$$

Simplify

$$3(x + 2) - 4(x - 1) = 24$$

Distribute again

$$3x + 6 - 4x + 4 = 24$$

Combine like terms

$$-x + 10 = 24$$

Isolate by subtracting 10 from each side

$$-x = 24 - 10 = 14$$

Then we can convert -x into a positive via dividing both sides by -1

$$\dfrac{-x}{-1} = \dfrac{14}{-1}$$ $$x = -14$$

---

Rational Equations

Rational equations are those that contain one or more rational expressions. In the previous example we had constants as denominators, now we’ll take a look at variable denominators.

$$\dfrac{1}{x} = \dfrac{1}{5} + \dfrac{3}{2x}$$

First we get the least common denominator by combining all the denominators, x, 5 and 2x which equals 10x. Then we multiple both sides by 10x

$$10x\left(\dfrac{1}{x}\right) = 10x\left(\dfrac{1}{5} + \dfrac{3}{2x}\right)$$

Distribute to each rational

$$10x \cdot \dfrac{1}{x} = 10x \cdot \dfrac{1}{5} + 10x \cdot \dfrac{3}{2x}$$

Divide out common factors

Find common factors

$$10x \cdot \dfrac{1}{x} = (5 \cdot 2x) \cdot \dfrac{1}{5} + (5 \cdot 2x) \cdot \dfrac{3}{2x}$$

Cancel those hoes out

$$10\cancel{x} \cdot \dfrac{1}{\cancel{x}} = (\cancel{5} \cdot 2x) \cdot \dfrac{1}{\cancel{5}} + (5 \cdot \cancel{2x}) \cdot \dfrac{3}{\cancel{2x}}$$

Left with the loyal ones

$$10 \cdot \dfrac{1}{1} = 2x \cdot \dfrac{1}{1} + 5 \cdot \dfrac{3}{1}$$

Simplfy

$$10 = 2x + 5 \cdot 3$$ $$10 = 2x + 15$$

Get the var on one side by subtracting the 15 from both sides

$$-5 = 2x$$

Divide the coefficient to transfer it to the left side

$$\dfrac{-5}{2} = -\dfrac{5}{2} = x$$

---

An equation that is true for all real numbers for which both sides are defined is called an identity, e.g. $x + 3 = x + 2 + 1$. No matter what number you put in here both sides of the expression are the same. The same is true about $\dfrac{2x}{x} = 2$.

A conditional equation is only an identity for at least one real number, e.g. $2x + 3 = 17$ since x has to be 7.

An inconsistent equation is that is never true, e.g. $x = x + 7$ where the solution set is $\varnothing$, the empty set.

Solving a Formula for a Variable

To solve a formula for a variable it measn we need to rewrite the formula so that the variable is solated on one side of the equation. It doesn’t mean getting a numerical value for that variable. Treat the variable as the ony variable in the equation, like x, and the other variables as if they are numbers.

For example, solving for l in

$$2l + 2w = P$$

Sub 2w from both sides,

$$2l = P - 2w$$

Divide both sides by 2

$$\dfrac{\cancel{2} l}{\cancel{2}} = l = \dfrac{P - 2w}{2}$$

---

What if a the variable appears twice?

$$A = P + Prt$$

Since we have two Ps we can factor it out

$$A = P(1 + rt)$$

Reverse the multiplication by dividing the 1 + rt

$$\dfrac{A}{1(1 + rt)} = \dfrac{P\cdot \cancel{(1 + rt)}}{\cancel{1(1 + rt)}} = P$$

---

Complex Numbers

Complex numbers are the square roots w/ negatives and radicands, instead of real numbers! Remember, the sqrt of real numbers are never negative. Mathematicians created the imaginary number i to be a solution of the equation $x^2 = -1$. Complex numbers is based on adding multiples of i, such as 7i, to real numbers.

It can be formally defined as

$$i = \sqrt{-1}$$

Where

$$i^2 = -1$$

Using this imaginary unit i, we can express the sqrt of any negative number as a real multiple of i, e.g.,

$$\sqrt{-25} = \sqrt{-1}\sqrt{25} = i\sqrt{25} = 5i$$

Complex Numbers and Imaginary Numbers

We can represent the set of all numbers in the from

$$a + bi$$

Where,

• $a$ is the real number, named the real part
• $b$ is the imaginary part.
• If $b \not = 0$ then the complex number is an imaginary number, else its a real number.
• An imaginary number in the form of $bi$ is a pure imaginary number.

For example, an imaginary number

$$2 + 2i$$

or a real number,

$$3 = 3 + 0i$$

If a complex number is expressed in the standard form of $a + bi$ then it is simplified. If $i$ is a radical we write $a + ib$ bc the radical could be confused with having the i within the radicand.

Complex Number Operations

Since the simpliest form of a complex number is a binomial we can use theh same methods!

For addition or subtraction we can leverage the common factors of i, b and d

$$(a + bi) - (c + di) = (a + c) - (b + d)i$$

For multiplication and division, it’s using the same principles we’ve previously learned w/ common factor cancelation and distributive, etc. This is why fully understanding the fundamentals is so incredibly important!

---

Quadratic Equations

A quadratic equation in xis, called a second-degree polynomial equation bc of the sqrt exponent, generally written as

$$ax^2 + bx + c = 0$$

Zero-Product Principle

If the product of the algebraic expressions is zero then we can use the zero-product principle, where if AB = 0 the A or B equals 0.

For example,

$$x^2 - 7x + 10 = 0$$

Can be factored into,

$$(x - 5)(x - 2) = 0$$

Where

$$x - 5 = 0$$ $$x = 5$$

Or

$$x - 2 = 0$$ $$x = 2$$

And we confirm this by plugging in each x value and see if 0 = 0 is true.

Square Root Property

When we find an expression that is $$u^2 = d$$ we can solve it by using the sqrt property by first moving 0 to one side, by subtracting the d from both sides

$$u^2 - d = 0$$

Now if we sqrt the d then we get the difference of two squares

$$(u + \sqrt{d})(u - \sqrt{d}) = 0$$

And now we check for

$$u + \sqrt{d} = 0$$ $$u = -\sqrt{d}$$

Or

$$u - \sqrt{d} = 0$$ $$u = \sqrt{d}$$

Since the solutions only differ in sign, we an write them as $u = \pm \sqrt{d}$

Lets do an example,

$$9x^2 + 25 = 0$$

First we want to get the real number on the other side to simplify

$$9x^2 = -25$$

Then we want to get rid of the coefficient to isolate the x^2

$$\dfrac{\cancel{9} \cdot x^2}{\cancel{9}} = \dfrac{-25}{9}$$ $$x^2 = \dfrac{-25}{9}$$

Then we want to remove the exponent from x via the root. And ofc we need to apply it to the other side of the equation

$$\sqrt{x^2} = \sqrt{\dfrac{-25}{9}}$$

Notice how the identity of the right side is imaginary.

$$x = \sqrt{-\dfrac{25}{9}}$$

Therefore we can write is w/ the plus minus

$$x = \sqrt{\pm\dfrac{25}{9}} = \pm\dfrac{25}{9}i$$

We can simplify the rational further

$$x = \pm\dfrac{5}{3}i$$

Then we verify the example w/ our x value

$$9\left(\pm\dfrac{5}{3}i\right)^2 + 25 = 0$$

Rewrite it as the unsimplified so there is a commmon factor

$$\dfrac{\cancel{9}}{1} \cdot \left(\dfrac{25}{\cancel{9}}i^2\right) + 25 = 0$$

We’re left with

$$25i^2 + 25 = 0$$

Replace our imaginary number w/ -1

$$25(-1)^2 + 25 = 0$$

Therefore,

$$0 = 0$$

And our solution set is verified to be `$$\{\pm\dfrac{5}{3}i\}$$

Completing the Square

What if we cannot factor the trinoial?

We would need to convert the equation into an equivalent equation that can be solved using the square root property.

If $x^2 + bx$ is a binomial, then creating a perfect square is simply adding $\left(\dfrac{b}{2}\right)^2$ at the end of the expression. Thus,

$$x^2 + bx + \left(\dfrac{b}{2}\right)^2 = \left(x + \dfrac{b}{2}\right)^2$$

Here’s a visualisation of what completing the square looks like (s/o Eddie Woo’s Beautiful Visual Explanation of Completing the Square )

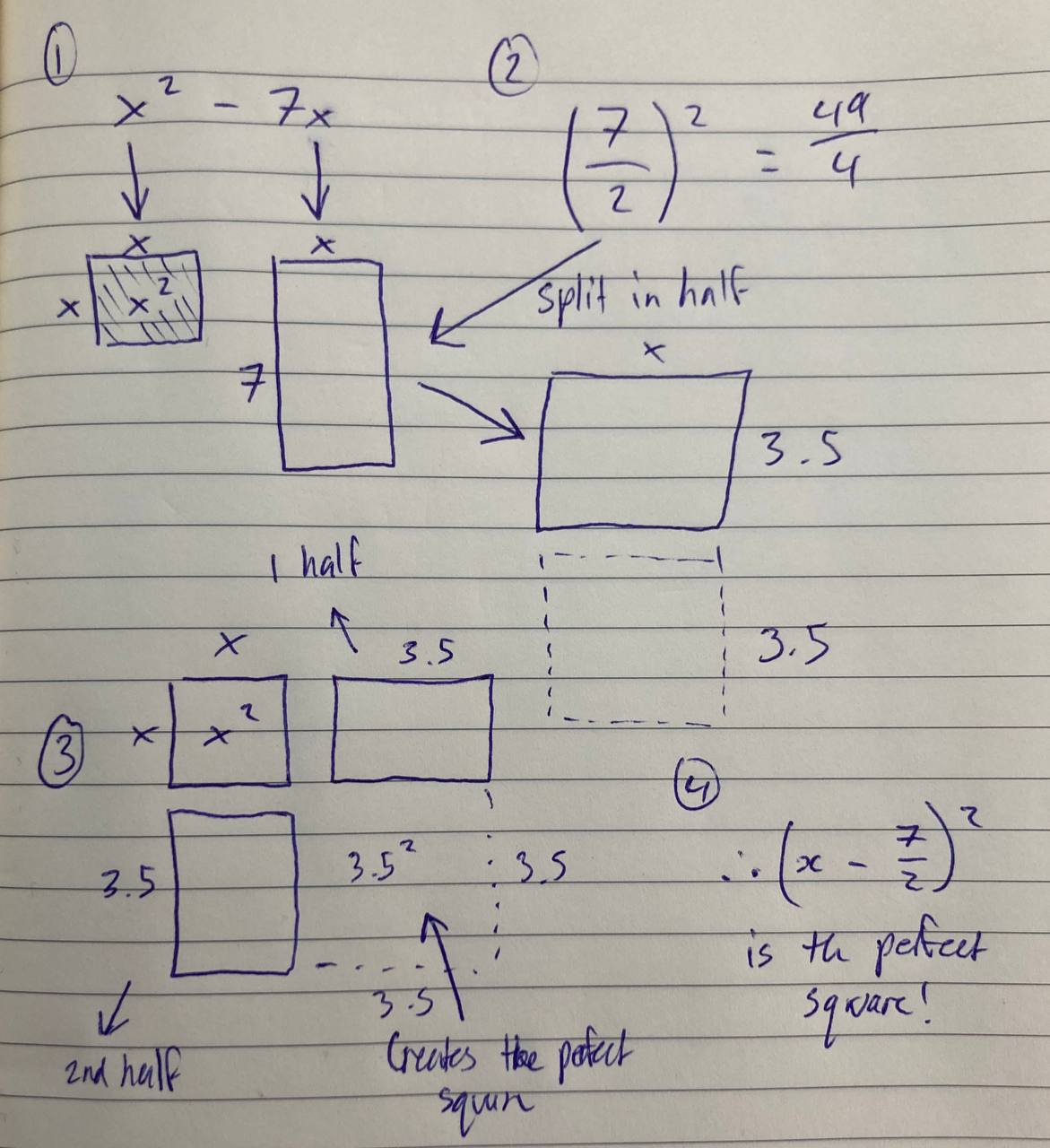
Deriving The Quadratic Formula

Using the method of completeing the square we can derive a formula that can be used to solve all quadratic equations.

$$ax^2 + bx + c = 0$$

Divide both sides by a to isolate x

$$\dfrac{\cancel{a} \cdot x^2}{\cancel{a}} + \dfrac{b}{a}x + \dfrac{c}{a} = 0$$

Isolate the binomial by adding $-\dfrac{c}{a}$ on both sides

$$x^2 + \dfrac{b}{a}x = -\dfrac{c}{a}$$

Notice how we can complete the square now! We 2a to double a so it’s half of a in relation to b. Don’t forget to apply to both sides too of the equation to keep the outcome the same.

$$x^2 + \dfrac{b}{a}x + \left(\dfrac{b}{2a} \right)^2 = -\dfrac{c}{a} + \left(\dfrac{b}{2a} \right)^2$$ $$x^2 + \dfrac{b}{a}x + \dfrac{b^2}{4a^2} = -\dfrac{c}{a} + \dfrac{b^2}{4a^2}$$

Remember from complete the square

$$\left(x \cdot \dfrac{b}{2a} \right)^2 = -\dfrac{c}{a} + \dfrac{b^2}{4a^2}$$

Find a common denominator on the right. We see that we have a and 4a^2 so we want to get the former to match the latter. Therefore we multiply a by 4a to get 4a^2, but that also means we need to multiply the numberator too! So c * 4a

$$\left(x \cdot \dfrac{b}{2a} \right)^2 = -\dfrac{c}{a} \cdot \dfrac{4a}{4a} + \dfrac{b^2}{4a^2}$$ $$\left(x \cdot \dfrac{b}{2a} \right)^2 = -\dfrac{4ac}{4a^2} + \dfrac{b^2}{4a^2}$$

Combine the like terms

$$\left(x \cdot \dfrac{b}{2a} \right)^2 = \dfrac{-4ac + b^2}{4a^2}$$

Move it around to not deal with negative numbers

$$\left(x \cdot \dfrac{b}{2a} \right)^2 = \dfrac{b^2 -4ac}{4a^2}$$

Get rid of the parentheses on the left side of the equation via sqrt, therefore we sqrt the right side

$$x \cdot \dfrac{b}{2a} = \pm \sqrt{\dfrac{b^2 -4ac}{4a^2}}$$

We can take the sqrt of the quotient, $4a^2$ -> $\sqrt{4a^2}$, simplifying the denominator,

$$x \cdot \dfrac{b}{2a} = \pm \dfrac{\sqrt{b^2 -4ac}}{2a}$$

Now we can remove $\dfrac{b}{2a}$ from the left side, and also the right side to simplify to it’s final form.

$$x = \dfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$$

And now we have the infamous *quadratic formula!

The Discriminant

In the quadratic formula,

$$x = \dfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$$

The $b^2 - 4ac$ is called the discriminant.

There are 3 different conditionals involving the discriminant that describes how many intercepts there are in a graph:

1. Two x-intercepts: $b^2 - 4ac > 0$
2. One x-intercept: $b^2 - 4ac = 0$
3. No x-intercepts: $b^2 - 4ac < 0$

Pythagorean Theorem

When thinking of a right triangle the hypotenuse will always be the sum of legs squared,

$$a^2 + b^2 = c^2$$

and we can simplify further

$$\pm \sqrt{a^2 + b^2} = \sqrt{c^2}$$

Since the distance is non-negative it would be

$$c = \sqrt{a^2 + b^2}$$

Midpoint Formula

What if we wanted to get the midpoint of the distance calculated w/ the pythagorean?

We would take the average of the both the coordinate pairs, i.e., we have $(x_1, x_2)$ and $(y_1, y_2)$ then we’d

$$\left( \dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2} \right)$$

Equations with Rationals Exponents

Exoressions with rational exponents represent radicals:

$$a^\frac{m}{n} = (\sqrt[n]{a})^m = \sqrt[n]{a^m}$$

A radical equation w/ rational exponents can be solved by:

1. Isolating the expression with the rational exponent, and
2. Raising both sides of the equatio nto a power that is the reciprocal of the rational exponent

For example,

$$x^\frac{3}{4} = 2$$

Apply the reciprocal of the left rational exponent to cancel them out, and apply to the other side

$$\left(x^\frac{3}{4}\right)^\frac{4}{3} = 2^\frac{4}{3}$$

Since the denominator is odd we don’t need the plus minus

$$x = 2^\frac{4}{3}$$

Lets do another example,

$$x^{\frac{2}{3}} - \dfrac{3}{4} = - \dfrac{1}{2}$$

First we add $\dfrac{3}{4}$ to both sides to isolate the x,

$$x^{\frac{2}{3}} = - \dfrac{1}{2} + \dfrac{3}{4}$$ $$x^{\frac{2}{3}} = \dfrac{1}{4}$$

Raise by sides by the reciprocal of the exponent. This cancels the left side exponent out bc they cancel each other out when cross canceling.

Since the original numerator is even, we need to use a plus minus,

$$\left(x^{\frac{\cancel2}{\cancel3}}\right)^\frac{\cancel3}{\cancel2} = \pm \left( \dfrac{1}{4} \right) ^ \frac{3}{2}$$ $$x = \pm \left( \dfrac{1}{4} \right) ^ \frac{3}{2}$$

Solving an Equation Quadratic in Form

This is quite interesting to build the mental model of what you can do in algebra.

If you have the equation,

$$x^4 - 8x^2 - 9 = 0$$

We can make this a quadratic equation by simplifying the x^4 by factoring

$$(x^2)^2 - 8x^2 - 9 = 0$$

Then we go further to remove the 8’s exponent via

$$u^2 - 8u - 9 = 0$$

Then we factor

$$(u - 9)(u + 1) = 0$$

And so u is either 9 or -1 and we can solve for u.

The point of showing you this example is to unlock the gate of manipulation in algebra.

---

Inequalities

Solving an inequatility is the process of finding a solution set that makes the inequatility true.

The first thing we need to know is interval notation.

Open interval $(a, b) = \{x | a < x < b \}$; the parentheses represents the loop range, excluding from the interval, e.g. 0-4 except elements 0 and 4 therefore $\{ 1, 2, 3 \}$

Closed interval $[a, b] = \{x | a \leq x \leq b \}$, is the same as open except the 0 and 4 are included! therefore $\{0, 1, 2, 3, 4\}$

The infinite interval $(a, \infin) = \{x | a > x \}$ is x + 1 until infinity. Something like $(-\infin, b] = \{x | x \leq b \}$ is everything before b.

Whenever you multiply or divide both sides of an inequatility by a negative number the direction of the inequality symbol is reversed, aka we change the sense of the inequality

Compound Inequalities

If we consider two Inequalities,

$$-3 < 2x + 1$$

And

$$2x + 1 \leq 3$$

We can express them as the compound inequality as

$$-3 < 2x + 1 \leq 3$$

This shorter form allows us to solve both inequalities at once!

By performing the same operation on all three parts of the inequality, our goal is to isolate x in the middle. Think as each < or > symbol as = and that anything you do to one side you must do to all the others, whether thats 1 or more.

For example,

$$-3 < 2x + 1 \leq 3$$

Sub 1 from all parts

$$-4 < 2x \leq 2$$

Isolate x by dividing all parts by 2

$$-2 < x \leq 1$$

Solving an Absolute Value inequatility

I want to show you one more before we move onto the next chapter.

Solving the solution set for

$$7 < |5 - 2x|$$

Initially, we can rewrite this as

$$|5 - 2x| > 7$$

Then to remove the abolsute value bars we can drop them as so,

$$5 - 2x > 7$$

And for the other side of the absolute it would be negative because it’s the opposite direction of the greater sign, which we established as > 7

$$5 - 2x < -7$$

So now we solve each inequalitiy separaetly then take the union of their solution sets.

Lets do the first,

$$5-2x < -7$$ $$-2x < -12$$

Divide and change sense of the inequalitiy

$$\dfrac{-2x}{-2} > {-12}{-2}$$ $$x > 6$$

And for the other,

$$5 - 2x > 7$$ $$- 2x > 2$$ $$\dfrac{-2x}{-2} < \dfrac{2}{-2}$$ $$x < -1$$

So our solution set is $\{ x | x < -1 || x > 6 \}$

Or in interval notation $(-\infin, - 1) \cup (6, \infin)$

---

Functions and Graphs 21/05/24

In a set of $\{ (10, 5), (11, 6) \}$ [10, 11] are the domains and [5,6] are the ranges.

A function is a correspondence from the domain (input set) to the range (output set). Each element in the domain corresponds to exactly one element in the range.

There are 2 types of variales,

• Independent, that don’t rely on anything.
• Dependent, that rely on others, e.g. in $y = x + 10$ y is depedent on x.

Fn Notation

Lets disect:

$$f(x) = -1.5x^2$$

• x is the input
• f(x) is the output
• = and everything follows is the equation
• if we supply f(10) then we’re evalutating the function at 10

If any vertical line intersects a graph in more than one point, the graph doesn’t define y as a function of x.

Observing Graphs

To prepare for calculus limits we want to know how to read graphs to get info from them.

There are 3 things to keep in mind,

1. A closed dot means the graph doesn’t go beyond that point and the point belongs to the graph
2. An open dot means the same as a closed dot except it doens’t belong to the graph
3. An arrow means the graph extends indefinitely in the direction it points

You’ll see in calculus that limits use the open and close all the time

There are two notions we’d use for identifying domaon and range from a fn’s graph:

Set-builder notion

$$\{ x | -4 \leq x \leq 2 \}$$

And the equiavelent interval notion

$$[-4, 2]$$

These two mean the exact same thing.

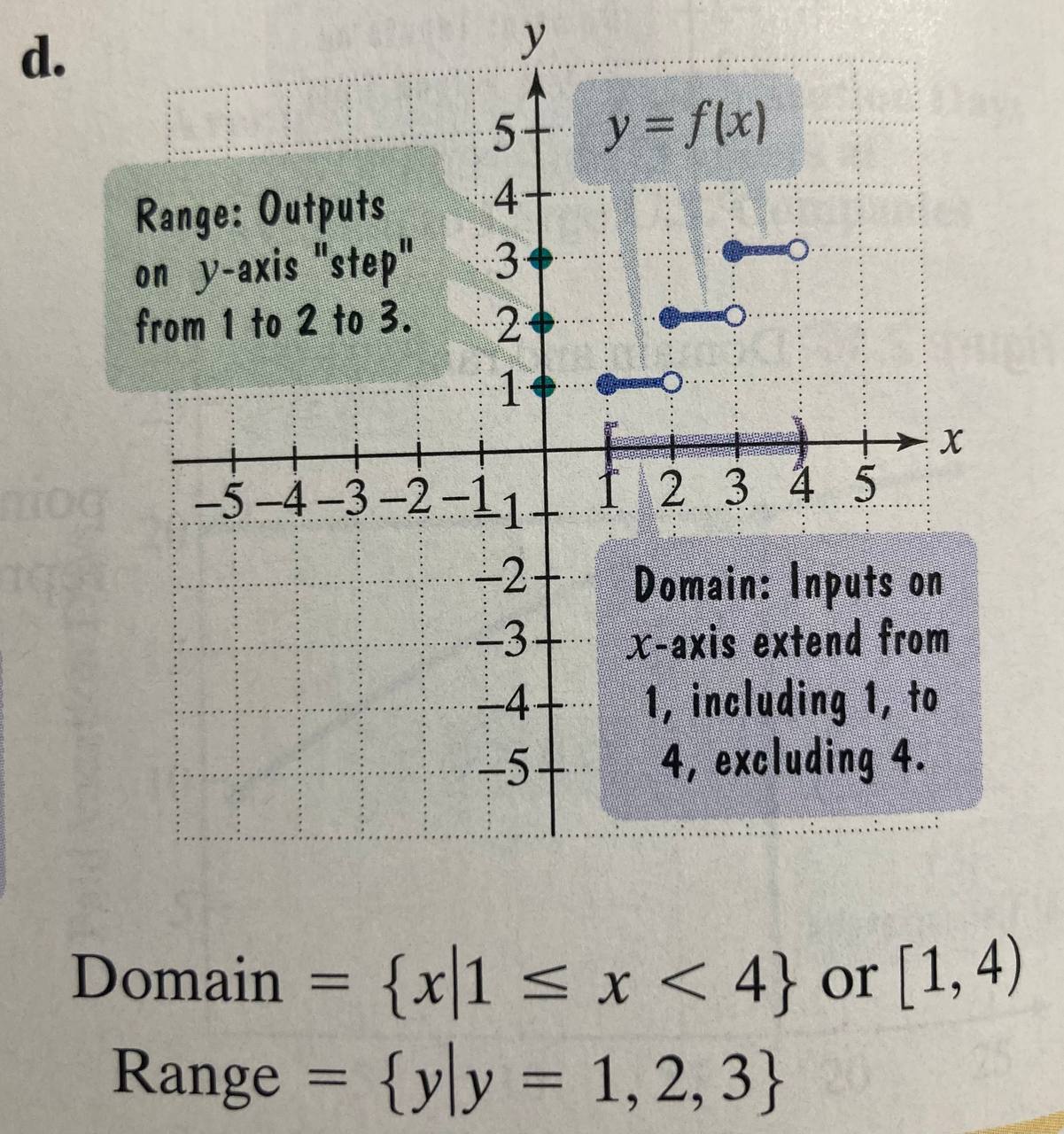
From here we see that the input set (range) are all on the y axis and the output set (domain) goes from 1 to 4, but not including 4 bc of the open dot!

Difference Quotients

To understand the average rate of change of a function we need to know this ratio called the difference quotient.

But why would we want to learn this?

It’s a stepping stone for calculus, the study of rates of change, since it builds the core concept of analysing changes.

Essentially, the difference quote tells us how much has changed w/ h from our initial point, x:

$$\dfrac{f(x + h) - f(x)}{h}$$

Lets do an example, if $f(x) = 2x^2 - x + 3$ find $f(x + h)$

Lets accomodate the former for the latter

$$f(x) = 2x^2 - x + 3$$

Into

$$f(x + h) = 2(x+h)^2 - (x+h) + 3$$

Lets distribute the $-(x+h)$ aka $-1(x+h)$

$$= 2(x+h)^2 - x - h + 3$$

Then distribute the $2(x+h)^2$ by distributing the exponent

$$= 2(x^2 + 2xh + h^2) - x - h + 3$$

Then distribute the coefficient

$$= 2x^2 + 4xh + 2h^2 - x - h + 3$$

Functions

Piecewise functions are fns that is defined by two or more equations over a specific input set (domain).

For example,

If t = 30 and we input it into

$$f(t) = \begin{cases} 20 &\text{if } 0 \leq t \leq 60 \\ 20 + 0.4(t - 60) &\text{if } t > 60 \end{cases}$$

The output for f(30) = 20. So think of a piecewise as a conditional if else function.

Local minimums are defined if there is a minimum lower than it’s own. And the reverse ofr local maximums. Globals are defined as the highest or lowest point found. This is important to understand in ML bc you’re trying to optimise for globals.

Slope

The slope measures the steepness of a line. This is quite important for calculus as we’d be measuring how this line changes over a period of time.

To measure the difference you use new position - initial position and it gives you the hypotenuse of the right angle triangle.

But the important part is always doing the change in y in the numerator.

We do this bc if we had the y change in the denominator it would be an completely inaccurate number, e.g. if y = 6 and x = 2 then clearly x/y != y/x w/ $\dfrac{2}{6} \not = \dfrac{6}{2}$

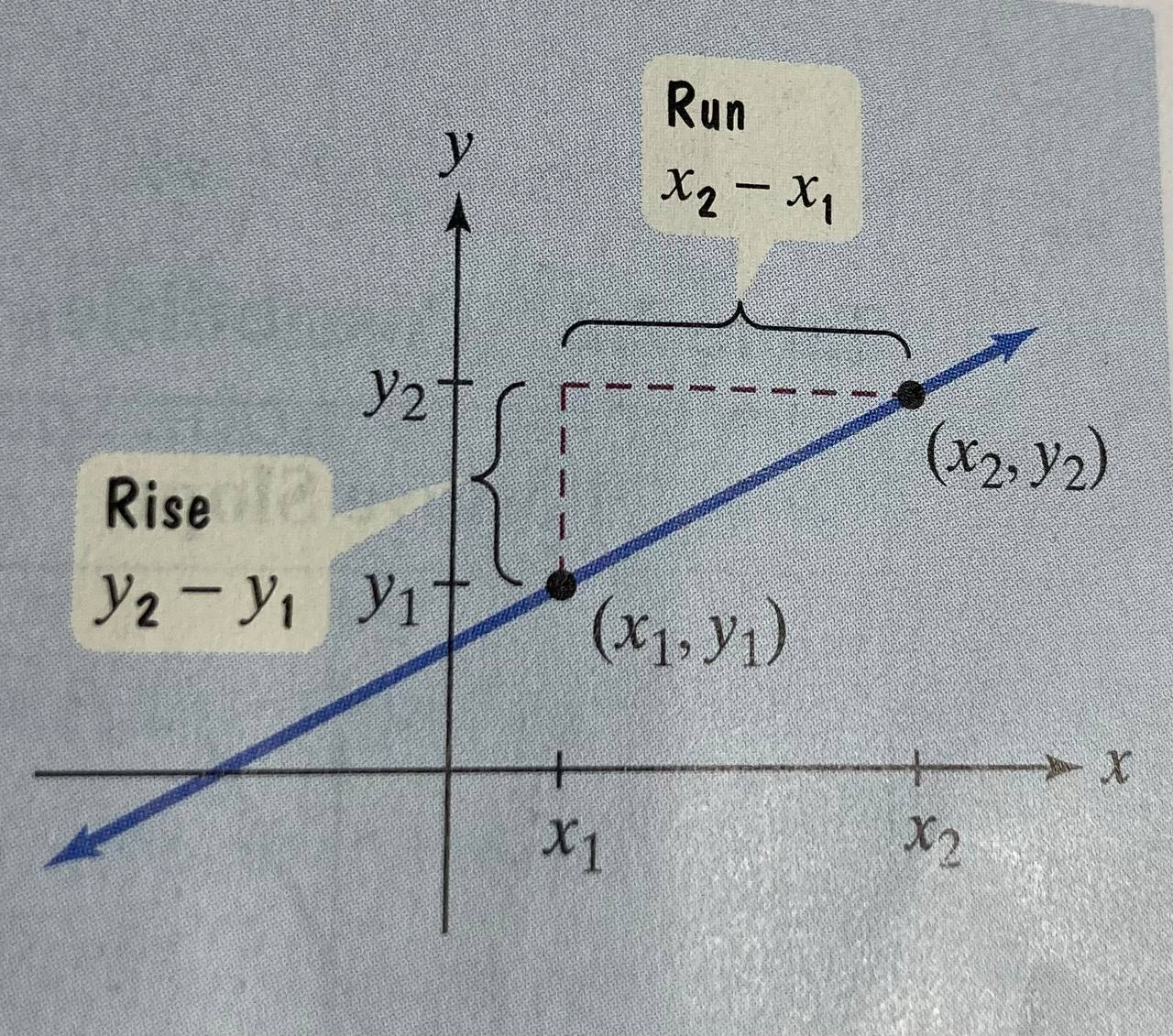
We can get the slope (m)‘s from,

$$m = \dfrac{y - y_1}{x - x_1}$$

If we wanted to get a specific point of y change from x change we cancel and apply to the other side

$$m(x - x_1) = \dfrac{y - y_1}{\cancel{x - x_1}} \cdot \cancel{(x - x_1)}$$

And we get our corresponding y change domain for x change

$$m(x - x_1) = y - y_1$$

This is called the point-slope form of the equation of a line

Lets say $x_1 = 0$ and $y_1 = b$

$$m(x - 0) = y - b$$

Simplify it to

$$mx = y - b$$

Then we add b to both sides to isolate y

$$mx + b = y$$

Or, as rearranged as

$$f(x) = y = mx + b$$

Functions in this form are called linear functions, where b is always a constant and mx is how steep that change is.

If the slope is 0 (horizontal line) then the equation really is just $y = b$.

General Form of The Equation of a Line

Every line has an equation that can be expressed as 1x + 0y - 5 = 0, or x - 5 = 0.

$$Ax + By + C = 0$$

For example, to convert the following into y = mx + b

$$3x + 2y - 4 = 0$$

We want ot isolate the 2y by moving the 4

$$3x + 2y = 4$$

Then the 3x

$$2y = -3x + 4$$

Then reverse the multiplication

$$y = \dfrac{-3x + 4}{2} = \dfrac{-3x}{2} + 2$$

Transformations of Functions

When we think of y = f(x) + c, when c is positive it tends to shift the graph upwards and vice versa for subtraction. By shifted up or down I mean it’s the graph visually hasn’t changed, it’s only vertically shifted up or down by b amount.

We can move it horizontally by y = f(x + c) where c dictates it’s horizontal positioning.

If we want to reflect out graph vertically can simply y = -f(x) to reverse the representation of it. To do the same for the horizontal plane we would put that subtraction operator in the fn as y = f(-x)

We can continue to morph though!

This time we’ll be modifying the graph’s basic shape by shrinking or enlarging it via y = cf(x). If c > 1 then the graph will stretch otherwise if 1 > c > 0 then the graph structure will shrink. And ofc to do it horizontally will be y = f(cx) where c > 1 will shrink it horizontally and the opposite will stretch.

Function Domains

If a fn f doesnt model data or verbal conditions, its domain is the largest set of real numbers that the value of f(x) is a real number. We exclude real numbers that cause division by zero and those that result in a square root of a negative number.

For example,

$$g(x) = \dfrac{3x + 2}{2^2 -2x - 3}$$

Since we have division we will say the denominator is 0 to be left with

$$g(x) = 2^2 -2x - 3 = 0$$

Then we factor

$$(x + 1)(x -3) = 0$$

Solve for left

$$x + 1 = 0$$ $$x = -1$$

Solve for right

$$x - 3 = 0$$ $$x = 3$$

So we must exclude -1 and 3 from the domain of g, resulting in the domain

$$= (-\infin, -1) \cup (-1, 3) \cup (3, \infin)$$

Fn Composition

When you form a composite function you “compose” two functions to form a new function.

The compoisition of the function f with g is denoted by $f \circ g$

$$(f \circ g)(x) = f(g(x))$$

You can think of the circle as the former encapsilating the latter. f is dependent on the domain g(x) has, like a bottleneck.

Inverse Fns

The inverse function denoted as $f^{-1}$, read as “f-inverse”, undoes the changes produced by $f$.

If we had $f(f^{-1}(x)) = x$ then $f^{-1}(f(x)) = x$.

A function has an inverse if there is no horizontal line that intersects the graph of f at more than one point.

Lets say function $f$ has the set of ordered pairs $(x, y)$ then the f-inverse would have $(y, x)$

If we wanted to find the inverse of

$$f(x) = 7x - 5$$

We would replace f(x) with y and solve for it

$$y = 7x - 5$$

Interchange x and y to get the inverse function

$$x = 7y - 5$$

Solve for y

$$x + 5 = 7y$$ $$\dfrac{x + 5}{7} = \dfrac{\cancel{7}y}{\cancel{7}} = y$$

Therefore, the inverse of $f(x) = 7x - 5$ is

$$f^{-1}(x) = \dfrac{x + 5}{7}$$

---

Polynomial and Rational Functions

Quadtraic Functions

We know from before that quadratic equations are represented as

$$f(x) = ax^2 + ax + c$$

The graph of any quadratic function is a parabola, which are shaped like cups. If the coefficient of $x^2$ is positive the parabola opens upward and the Vertex is at the bottom, and the reverse for if it’s negative w/ the vertex at the top.

The standard form of a quadratic function is

$$f(x) = a(x - h)^2 + k, a \not = 0$$

• If a > 0 the parabola opens upwards
• The vertex is (h, k)
• If h > 0 the graph is shifted h units to the right
• If k > 0 the graph is shifted k units up

You find the intercept by solving $f(x) = 0$ and manipulating x to find it’s values.

For example,

$$f(x) = -2(x - 3)^2 + 8$$

We see that the coefficient is a negatitve so it tells us the parabola opens downwards and the vertex is (h, k) or in our case (-3, 8).

So we find the x-intercepts by replacing f(x) w/ 0. Lets go through that,

$$0 = -2(x - 3)^2 + 8$$

We reverse the negative coefficient by adding the opposite to both sides

$$2(x - 3)^2 = 8$$

Divide both sides by 2 to remove the coefficient

$$\dfrac{2(x - 3)^2}{2} = \dfrac{8}{2}$$

Then we apply the sqrt property to get

$$x - 3 = \sqrt{4} = 2$$ $$x = \sqrt{4} = 5$$

And

$$x - 3 = -\sqrt{4} = -2$$ $$x = -\sqrt{4} = 1$$

And now our x-intercepts are 1 and 5 where the parabola passes through (1,0) and (5,0).

Note, if you cannot solve for the x-intercepts by factoring use the quadratic formula.

We find the y-intercept by computing for f(0), so

$$f(x) = -2(x - 3)^2 + 8$$

is turned into

$$f(0) = -2(0 - 3)^2 + 8$$ $$= -2(-3)^2 + 8$$ $$= -2(9) + 8$$ $$= -10$$

And so the y-intercept is -10, where the parabola passed through (0, -10).

Parabola Vertex

If we wanted to find the parabola’s vertex from the quadratic function

$$f(x) = ax^2 + bx + c$$

then we would complete the square by first factoring out a

$$= a \left (x^2 + \dfrac{b}{a}x \right) + c$$

Then we complete the square by adding the sqaure of half the coefficient of x

$$= a \left (x^2 + \dfrac{b}{a}x + \dfrac{b^2}{4a^2}\right) + c$$

And by completing the square we need to add $a \cdot \dfrac{b^2}{4a^2}$. To avoid changing the function’s equation we must subtract this term.

$$= a \left (x^2 + \dfrac{b}{a}x + \dfrac{b^2}{4a^2}\right) + c - a \dfrac{b^2}{4a^2}$$

We rewirte the trinomial as the square of a binomial and simplify the constant term

$$= a \left( x + \dfrac{b}{2a} \right)^2 + c - \dfrac{b^2}{4a}$$

And then we plug it into the standard form

$$f(x) = a \left( x - \left( - \dfrac{b}{2a} \right) \right)^2 + c - \dfrac{b^2}{4a}$$

And so the parabola’s vertex $(x_1, x_2)$ is

$$\left (-\dfrac{b}{2a}, f(-\dfrac{b}{2a}) \right)$$

Polynomial Functions

From the beginning we know polynomials are expressions w/ terms.len >= 3 with the leading coefficient being the term with the largest exponent, aka the degree.

So, a polynomial function looks like this

$$f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0$$

These graphs are smooth (rounded curves w/ no sharp corners) and continuous (no breaks without lifting your pencil).

Wen we get into calculus we’ll mostly be dealing with polynomial functions and then trying to discover the rate of change from one part of the squiggly line to another.

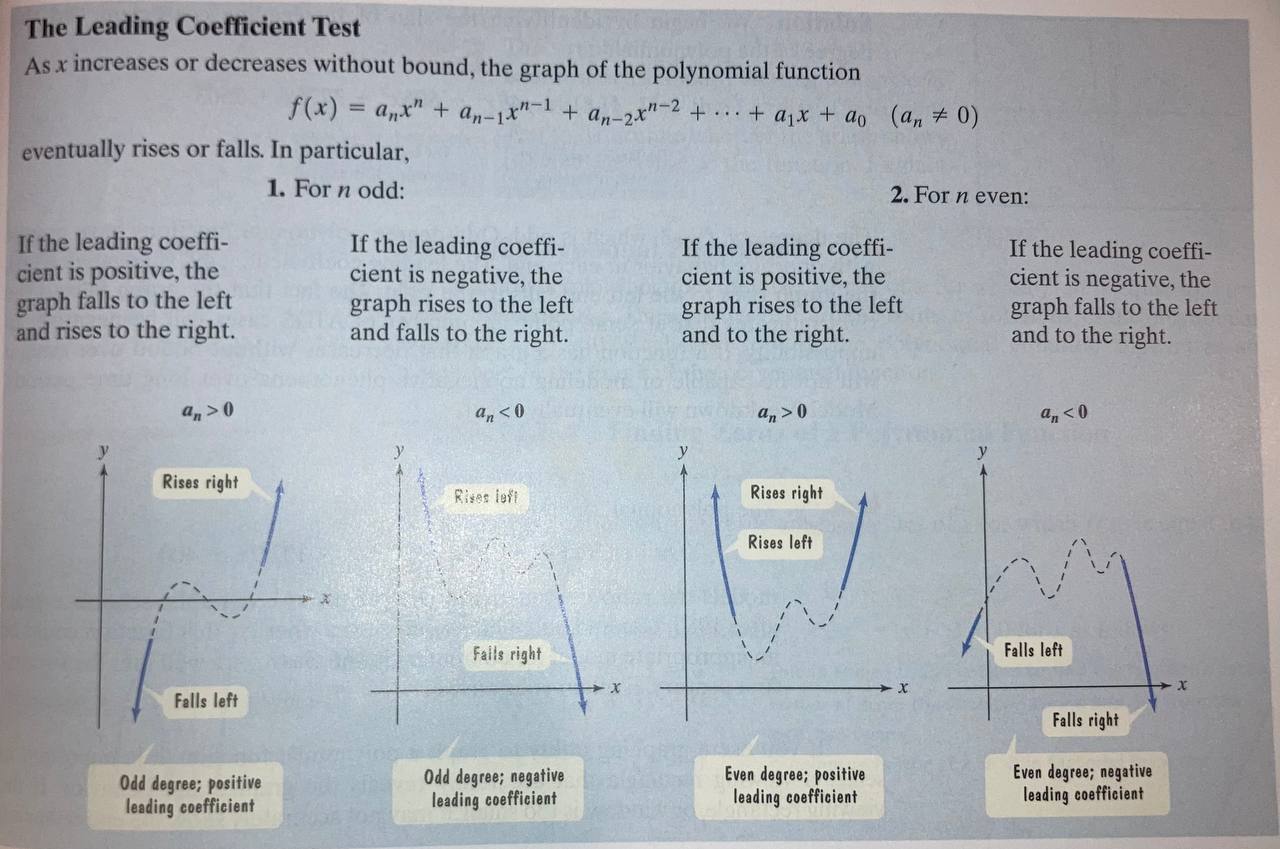
Wen describing the behaviour of a graph of a function to the far left or the far right we call it it’s end behaviour.

We can determining whether the end of the graph goes up or down at the end by it’s leading coefficient.

Zeros of Polynomial Functions

When we want to find the x-intercept points that land on zero we solve our polynomial fn for zero f(x) = 0.

For example,

$$f(x) = x^3 + 3x^2 - x - 3$$

Becomes

$$f(x) = x^3 + 3x^2 - x - 3 = 0$$

First we factor $x^2$ from the first two terms and -1 from the last two terms

$$x^2(x+ 3) - (x + 3) = 0$$

Notice how we have a common factor of 3, so we factor it too

$$(x+3)(x^2-1) = 0$$

Then we set each factor to 0, First

$$x+3 = 0$$ $$x = -3$$

Second

$$x^2-1 = 0$$ $$x^2 = 1$$

Remember that if $x^2 = d$ then $x^2 = \pm \sqrt{d}$

$$x = \pm 1$$

And so, now we know the zeros of f are [-3, -1, 1] or [(-3, 0), (-1, 0), (1, 0)].

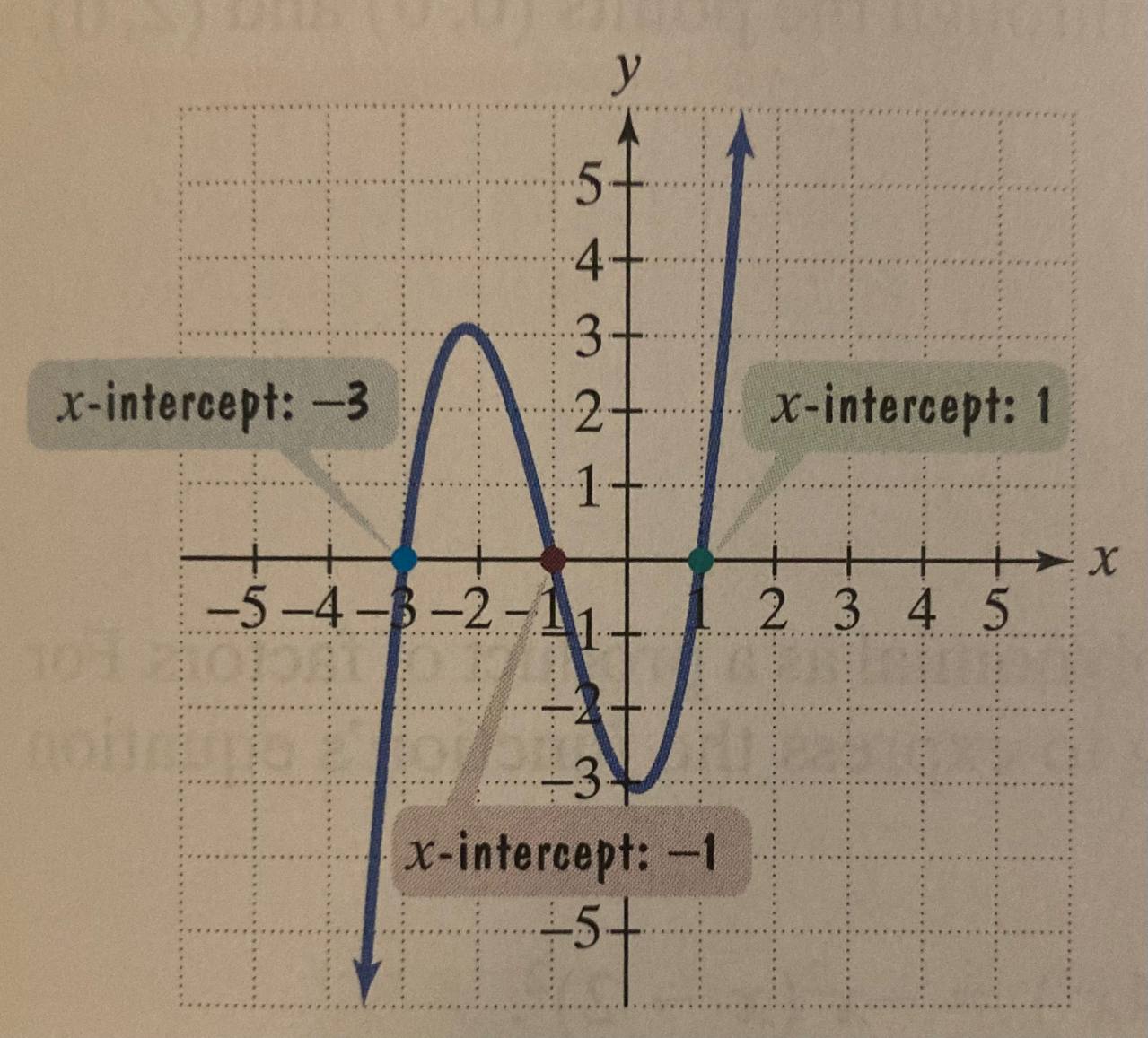
Multiplicities of Zeros

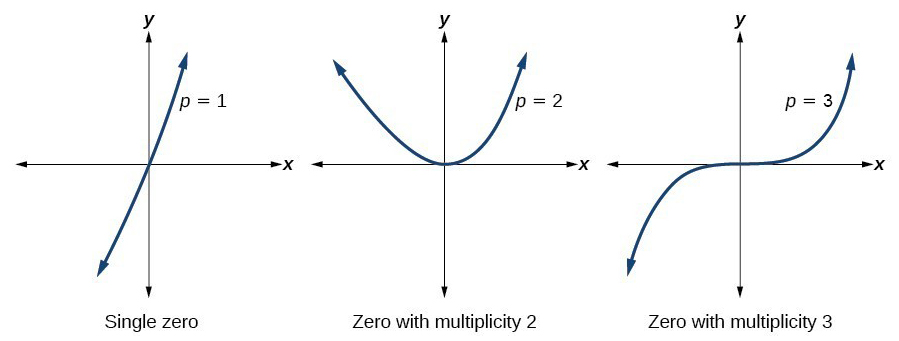
The multiplicities of zeros of the x-intercepts tells us the curvature of the graph:

1. if even then it touches the x-axis and turns back around, like a U-turn
2. if it’s odd then it grosses the x-axis
3. the higher the multiplicity of zero the more flat it becomes

Dividing Polynomials

Polynomials are super important as fundamental building blocks of math. So we need to know how to apply division to a polynomial function.

Luckily, we iterate a four step formula to get through this daunting task:

1. Divide
2. Multiply
3. Subtract + flip sign
4. Bring down the next term in the polynomial

So wtf does it mean? Lets do an example

Divide $4 - 5x - x^2 + 6x^3$ by $3x - 2$

First we can rearrange the expression in descending powers of x

$$6x^3 - x^2 - 5x + 4$$

Then we divide 6x^3 by our first term in the divisor 3x, $\dfrac{6x^3}{3x}$ aka $\dfrac{6 \cdot x \cdot x \cdot \cancel{x}}{3 \cdot \cancel{x}} = 2x^2$

We then multiply that result, $2x^2$ by the entire divisor $2x^2(3x - 2)$ which gives us $6x^3 - 4x^2$

And now we subtract the first two terms of the original expression by the new binomial, $6x^3 - 4x^2$.

But there’s a twist! We need to change the signs of the polynomial being subtracted

$$(- 6x^3 + 4x^2) + (6x^3 - x^2)$$ $$= (\cancel{-6x^3} + 4x^2) + (\cancel{6x^3} - x^2)$$ $$= 4x^2 - 1x^2$$ $$= 3x^2$$

Then we move the next term in the original polynomial down to create the expression. So we already used the first 2 elements so we bring down the 3rd element, -5x

$$3x^2 - 5x$$

And we run through the same foru steps again. Starting with the 3x divisor term division

$$\dfrac{3x^2}{3x} - 5x$$ $$x - 5x$$

Then multiply by the divisor

$$x(3x - 2)$$ $$3^2 - 2x$$

Then we subtract, but flipping the sign

$$(-3^2 + 2x) + (3x^2 - 5x)$$ $$(\cancel{-3^2} + 2x) + (\cancel{3x^2} - 5x)$$ $$2x - 5x$$ $$-3$$

And we bring the last term down +4 which gives use

$$-3x + 4$$

And finally we do the last four step iteration

$$\dfrac{-3x}{3x} + 4$$ $$-1 + 4$$

Multiply by divisors

$$-1(3x - 2)$$ $$-3x + 2$$

Subtract and flip one last time

$$(+3x - 2) + (-3x + 4)$$ $$(\cancel{+3x} - 2) + (\cancel{-3x} + 4)$$ $$- 2 + 4$$

And we get a remainder of 2

$$2$$

Therefore, the found quotient is

$$2x^2 + x - 1$$

Where each term is from the division from each step, with a remainder of 2 from solving it.

Whenever there is a non-zero remainder we must list the quotient plus the remainder above the divisor,

$$\dfrac{6x^3 - x^2 - 5x + 4}{3x - 2} = 2x^2 + x - 1 + \dfrac{2}{3x - 2}$$

Now, this process is called the Division Algorithm

$$f(x) = d(x) \cdot q(x) + r(x)$$

Where,

• f(x) is the function
• d(x) is the divisor
• q(x) is the quotient
• r(x) is the remainder

Synthetic Division

Now that we’ve done the extremely long and painful division lets learn the shortcut version!

If the divisor has the form of $x - c$ then we’re able to use this quick and easy strat that gets us the quotient significantly faster than long divison.

For example, lets divide the following by $x - 3$

$$x^3 + 4x^2 - 5x + 5$$

We view this as 3 being the mutiplier and

• [1, 4, -5, 5]

First, we bring the first coefficient 1 in our new expression

• [1, 4, -5, 5]
• [_, _, _, _]
• [1, _, _, _]

For the second element we multiply 1 by 3

• [1, 4, -5, 5]
• [_, 3, _, _]
• [1, _, _, _]

Then we add 4 + 3

• [1, 4, -5, 5]
• [_, 3, _, _]
• [1, 7, _, _]

Then 3 * 7 = 21 to create the 2nd row’s 2nd element

• [1, 4, -5, 5]
• [_, 3, 21, _]
• [1, 7, _, _]

Subtracting 21 - 5 = 16

• [1, 4, -5, 5]
• [_, 3, 21, _]
• [1, 7, 16, _]

Same thing by multiplying 16 * 3 = 48 then adding 48 + 5 = 53

• [1, 4, -5, 5]
• [_, 3, 21, 48]
• [1, 7, 16, 53]

And now we convert [1, 7, 16, 53] into the following expression where the degree of the first term of the quotient is one less than the degree of the first term of the dividend and the final value is the remainder,

$$1x^2 + 7x + 16 + \dfrac{53}{x - 3}$$

Remainder Theorem

Interesting enough, when we consider the Division Algo when the dividend, f(x), is divided by x - c and we solve for f(c) then the expression goes from

$$f(x) = (x - c) \cdot q(x) + r$$

To

$$f(c) = (c - c) \cdot q(c) + r$$ $$= 0 + r$$ $$= r$$

Factor Theorem

But what if f(c) = 0 in f(x) = (x-c)q(x) + f(c)?

Then we have

$$f(x) = (x - c) \cdot q(c)$$

Meaning x - c is a factor of $f(x) = (x - c) \cdot q(c)$

So if we replace x in $f(x) = (x - c) \cdot q(c)$ w/ c we get

$f(c) = (c - c) \cdot q(c) = 0$

Meaning,

1. If f(c) = 0 then x - c is a factor of f(x)
2. If x - c is a factor of f(x) then f(c) = 0

Rational Zero Theorem

This theorem tells us all possible rational zeros of a polynomial function w/ the formula,

$$\text{Possible rational zeros} = \dfrac{\text{Factors of the constant term}}{\text{Factors of the leading coefficient}}$$

So for example, listing all the possible rational zeros of $f(x) -x^4 + 3x^2 + 4$ would be

$$= \dfrac{\text{factors of 4}}{\text{factors of -1}}$$ $$= \dfrac{\pm 1, \pm 2, \pm 4}{\pm 1} = \pm 1, \pm 2, \pm 4$$

Rational Functions

To extend polynomial functions, we have rational functions at are quotients of polynomial functions! They are expressed as

$$f(x) = \dfrac{p(x)}{q(x)}$$

Where p and q are polynomial functions. The domain is the set of all real numbers that make the denominator zero.

For example, the domain of

$$f(x) = \dfrac{x^2 + 7x + 9}{x(x - 2 )(x + 5)}$$

Would be all real numbers except $\{ 0, 2, -5 \}$

Arrow Notation

As we approach calculus we’ll be seeing this more frequently in limits. But for now just know,

• $a \rarr a^{+}$: x approaches a from the right
• $a \rarr a^{-}$: x approaches a from the left
• $a \rarr \infin$: x approaches infinity (increasing without bound)
• $a \rarr -\infin$: x approaches infinity (decreasing without bound)

Asymptotes

If x = a then we have a vertical asymptote.

For example, to find the vertical asymptote of

$$f(x) = \dfrac{x + 3}{x^2 - 9}$$

we need to attempt to find common factors

$$f(x) = \dfrac{\cancel{(x + 3)}}{\cancel{(x + 3)}(x - 3)}$$ $$= \dfrac{1}{x - 3}$$ $$x = 3$$

Therefore, our vertical asymptote is at x-axis 3

But what if we inversed the subtraction operation?

$$f(x) = \dfrac{x + 3}{x^2 + 9}$$

Then there wouldn’t be any real numbers to make the denominator 0, thus it has no vertical asymptotes!

To find the horizontal asymptote we simply observe the degree of the numerator and denominator in

$$f(x) = \dfrac{a_nx^n, ..}{b_mx^m, ..}$$

1. If n < m then y = 0 is the horizontal asymptote
2. If n = m then the line $y = \dfrac{a_n}{a_m}$ is the horizontal asymptote
3. If n > m there is no horizontal asymptote

However, we get a slant asymptote if the degree of the numerator is one more than the degree of the denominator, e.g., $f(x) = \dfrac{x^2 + 1}{x - 1}$

Polynomial Inequalities

When we’re given a polynomial like

$$f(x) = 1.2x^2 + 15.2x + 181.4 > 500$$

Sub 500 from both sides

$$= 1.2x^2 + 15.2x + 181.4 - 500 > 500 - 500$$ $$= 1.2x^2 + 15.2x -318.6 > 0$$

Now we have a polynomial inequalitiy! Which can be defined as either

• $f(x) < 0$
• $f(x) > 0$
• $f(x) \geq 0$
• $f(x) \leq 0$

---

Exponential & Logarithmic Functions

Exponential functions differ from polynomial functions by containing a variable in the exponent while having the base be positive, e.g. $f(x) = 12(0.1)^x - 1$ ($12(0.1)$ is the base) but $H(x) = (-1)^x$ is not an exponential fn.

Logarithmic functions are the inverse of exponential functions. So there is an inverse property too:

When we want to evaluate something like

$$log_4 4^5$$

Then we think of the exponent first of

$$4^5 = 20$$

And then the log of it is really saying “what exponent do we give 4 that results in 20?” which is 5.

$$log_4 20 = 5$$

When representing as a function, we can say the exponential form expression is

$$f(2) = 8^2 = 16$$

and the inverse form, the Logarithmic form, as

$$f^{-1}(2) = \log_2 16 = 8$$

---

For another example, that uses the inverse property of logs + exponents lets evaluate

$$10^{\log_{10} 100}$$

First we can calculate the $\log_{10} 100$

$$\log_{10} 100 = 2$$

Because

$$10^2 = 100$$

Therefore,

$$\log_{10} 100 = 10^2 = 100$$

So we can say the exponent of x in $b^{\log_{b} x}$ or the inverse form $\log_{b} b^{x}$ is always the answer.

---

Natural Log

There’s a log that’s used so often that it’s given it’s own symbol, the natural logarithm $$\ln$$

where the base is $e$ which is an irrational and transcendental number approximately equal to 2.71828. It’s named the “natural log” bc it has several important properties and applications in mathematics, science, and engineering — we’ll find this pop in calculus.

Common Log

The common log is a log with a base, 10 that used so often it’s referred to the common log.

Properties of Logarithms

This should be quite intuitive but we’ll go through It

For each of these we would say we are “expanding a logarithmic expression”

1. Product rule (sum): $\log_b(MN) = \log_bM + log_bN$
2. Quotient rule (difference): $\log_b\left(\dfrac{M}{N}\right) = \log_bM - log_bN$
3. Power rule (exponent): $\log_b{M^P} = p \log_bM$
   • E.g, $log_2x + log_2(x - 7) = 3$ can be solved from $log_2\begin{bmatrix} x(x - 7) \end{bmatrix} = 3$ and in exponential form as $log_bM = c$ means $b^c = M$ we can rewrite as $2^3 = x(x - 7)$

If we wanted to change our base, such as the natural logarithm $e$ (base 10), to another we would use the expression

$$\log_b M = \dfrac{\log_a M}{\log_a b}$$

Where $b$ is the original base and $a$ is the new base

---

Exponental Equations

An exponential equation is an equation that has a variable in the exponent, e.g.

$$27^{x + 3} = 9^{x - 1}$$

Bc $27 = 3^3$ and $9 = 3^2$ therefore we can write each side as a power of the same base, 3

$$(3^3)^{x + 3} = (3^2)^{x - 1}$$

When an exponential expression is raised to a power, multiply exponents

$$3^{3 (x + 3 )} = 3^{2(x - 1)}$$

If the two bases are equal then the two exponents are equal, so we can remove the bases

$$3(x + 3 ) = 2(x - 1)$$

Then we apply the distributive property

$$3x + 9 = 2x - 2$$

Sub 2x from both sides

$$x + 9 = - 2$$

Then sub then 9 from both

$$x = -11$$

So the solution set is

$$\{ -11 \}$$

Using Natural Logs to Solve Exponential Equations

Most exponential equations cannot be rewritten so that each side hhas the same base. Logs are extremely useful for solving these.

Lets learn by solving

$$4^x = 15$$

Since the exponential express $4^x$ is already isolated we can take the natural log from both sides

$$\ln 4^x = \ln 15$$

We can use the power rule property to move the variable exponent to the front

$$x \ln 4 = \ln 15$$

And we can move the $\ln 4$ to the other side by dividng both sides to get our solution set

$$x = \dfrac{\ln 15}{\ln 4}$$

---

Logarithmic Equations

A logarithmic equation is one that contains a variable in a logarithmic expression.

Again, lets learn by example,

$$3 \ln(2x) = 12$$

We can start by dividng by sides by 3

$$\ln(2x) = 4$$

Rewrite in exponential form: $\log_bM = c$ means $b^c = M$

$$\ln^4 = 2x$$

You know the drill

$$\dfrac{\ln^4}{2} = x$$

Now we always check solutions of log equations in the original equation. If it’s a negative number or log of 0 then it’s discarded.

$$3 \ln \begin{bmatrix} 2 \left( \dfrac{\ln^4}{2} \right) \end{bmatrix} = 12$$

We can rewrite it as the following to make the next step more obvious

$$3 \ln \begin{bmatrix} \dfrac{\cancel{2}}{1} \cdot \dfrac{\ln^4}{\cancel{2}} \end{bmatrix} = 12$$

COMMON FACTOR BABY

$$3 \ln \ln^4 = 12$$

We can actually rewrite this as

$$3 \ln e^4 = 12$$

And bc $e^x = x$

$$3 \cdot 4 = 12$$

And so this is our result

$$12 = 12$$

Which confirms our solution set is

$$\left\{ \dfrac{e^4}{2} \right\}$$

---

One-to-One Property of Logs

To use the one-to-one property of logs, we need a single log whose coefficient is 1 on each side of the equation.

For example,

$$\ln (x + 2) - \ln(4x + 3) = \ln \left( \dfrac{1}{x} \right)$$

We can use the quotient rule $\log_bM - \log_bN = \log_b \left( \dfrac{M}{N} \right)$ to get a single log on the left side

$$\ln \left( \dfrac{x + 2}{4x + 3} \right) = \ln \left( \dfrac{1}{x} \right)$$

One-to-one property: if $\log_bM = \log_bN \text{ then } M = N$

$$\dfrac{x + 2}{4x + 3} = \dfrac{1}{x}$$

Multiply both sides by the LCD, $x(4x + 3)$

$$x\cancel{(4x + 3)} \left( \dfrac{x + 2}{\cancel{4x + 3}} \right) = \cancel{x}(4x + 3) \left( \dfrac{1}{\cancel{x}} \right)$$

Simplify

$$x + 2 = 4x + 3$$

Distribute

$$x^2 + 2x = 4x + 3$$

Sub 4x + 3 from both sides to set the equation to 0

$$x^2 - 2x - 3 = 0$$

Factor

$$(x - 3) (x + 1) = 0$$

And we get both

$$x = 3$$ $$x = - 1$$

x = -1 produces negative numbers so it’s not a solution, however 3 creates $\ln \dfrac{1}{3}$ so we gucci baby! The solution set is $\left\{ 3 \right\}$

---

Systems of Equations and Inequalities

A system of linear equations or a linear system is a multi-equation problem.

For example, ${ (3, 4) }$ satisfies the linear system

$$x + y = 7 \newline x - y = -1$$

as

$$3 + 4 = 7 \newline 3 - 4 = -1$$

But what if we didn’t have a graph to see this stuff (these two would be easily identifiable w/ a quadratic graph w/ 2 lines)?

Substituation Method

$$5x - 4y = 9 \newline x - 2y = -3$$

We start by solving either of the equations for one variable in terms of the other.

We begin by isolating one of the variables, lets start with the second’s x.

$$\begin{split} x - 2y &= -3 \\ x &= 2y - 3 \end{split}$$

Now we substitute the expression into the other equation, $5x - 4y = 9$ as x

$$\begin{split} 5(2y - 3) - 4y &= 9 \\ 10y - 15 - 4y &= 9 \\ 10y - 4y &= 9 + 15 \\ 6y &= 24 \\ y &= \dfrac{24}{6} \\ y &= 4 \end{split}$$

Then we use y = 4 in the original equations to get the x value

$$\begin{split} 5x - 4y &= 9 \\ 5x - 4(4) &= 9 \\ 5x - 16 &= 9 \\ 5x &= 9 + 16 \\ 5x &= 25 \\ x &= \dfrac{25}{5} \\ x &= 5 \end{split}$$

And

$$\begin{split} x - 2y &= -3 \\ x - 2(4) &= -3 \\ x - 8 &= -3 \\ x &= -3 + 8 \\ x &= 5 \\ \end{split}$$

And now our proposed solution set that satisfies both equations is $\{ (5,4) \}$

Addition Method

The substituation method is most useful if one of the given equations has an isolated variable.

But there is another method that enables us to quickly solve these linear systems.

Lets run through the example,

$$\begin{split} 3x + 2y &= 48 \\ 9x - 8y &= -24 \end{split}$$

Both equations are already in $Ax + By = C$ form, so we skip this step.

We want both equations to have either the sum of x-coefficients or y-coefficients to be zero. In our case, we will multiply the first equation by -3

$$\begin{split} - 9x - 6y &= -144 \\ 9x - 8y &= -24 \end{split}$$

Then we add the equations together. This is what gives it the name Addition Method

$$\begin{split} -14y &= -168 \\ \dfrac{\cancel{-14} \cdot y}{\cancel{-14}} &= \dfrac{-168}{-14} \\ y &= 12 \end{split}$$

Then we substitute and find the value of the other variable w/ this y value into either of the equations. We’ll choose the simpliest one

$$\begin{split} 3x + 2y &= 48 \\ 3x + 2(12) &= 48 \\ 3x + 24 &= 48 \\ 3x &= 24 \\ x &= \dfrac{24}{3} \\ x &= 8 \\ \end{split}$$

And our proposed solution set is $\{ (8, 12) \}$

---

We know if there is no solution, aka an inconsistent system, if you encounter a false statement, e.g. 69 = 420. This just means the 2 lines in the quadratic graph are parallel.

If the x and y values are the exact same then we have infinite solutions, meaning the two lines are identical, overlapping one another.

---

Three Variable Linear Systems

Using the methods we discussed, we can apply it to a 3 variable linear system.

For example,

$$\begin{split} 5x - 2y - 4z &= 3 \\ 3x - 3y + 2z &= -3 \\ -2x + 5y + 3z &= 3 \\ \end{split}$$

The goal here is to take two different pairs of equations and eliminate the same variable from both pairs.

So, our first step is to reduce the system into two equations in two variables.

$$\begin{split} 5x - 2y - 4z &= 3 \\ 3x - 3y + 2z &= -3 \\ \end{split}$$

We multiply the 2nd equation by 2 and don’t change the top to cancel out the z var

$$\begin{split} 5x - 2y - 4z &= 3 \\ 6x + 6y + 4z &= -6 \\ \end{split}$$

We add them together to get

$$\begin{split} 11x + 4y &= -3 \end{split}$$

Then we must eliminate the same var using another pair of equations. So this time we use the 2nd and 3rd equation, instead of the 1st and 2nd

$$\begin{split} 3x - 3y + 2z &= -3 \\ -2x + 5y + 3z &= 3 \\ \end{split}$$

We multiply the top by -3 and the bottom by 2

$$\begin{split} -9x - -9y + -6z &= 9 \\ -4x + 10y + 6z &= 6 \\ \end{split}$$

And add them together

$$\begin{split} -13x + y &= 15 \\ \end{split}$$

Our new equations gives us a system of two equations in two variables:

$$\begin{split} 11x + 4y &= -3 \\ -13x + y &= 15 \\ \end{split}$$

Lets solve for x first. Start by only multiplying the 2nd by -4

$$\begin{split} 11x + 4y &= -3 \\ 52x -4 y &= -60 \\ \end{split}$$

Add together

$$\begin{split} 63x &= -63 \\ x & = -1 \end{split}$$

Then we use the x in of the two new equations we have

$$\begin{split} -13x + y &= 15 \\ -13(-1) + y &= 15 \\ 13 + y &= 15 \\ y &= 2 \\ \end{split}$$

Then we use x = -1 and y = 2 in one of our original 3 equations,

$$\begin{split} 3x + 3y + 2z &= - 3 \\ 3(-1) + 3(2) + 2z &= - 3 \\ 3 + 2z &= - 3 \\ 2z &= -6 \\ z &= -3 \\ \end{split}$$

And our proposed solution set is $\{(-1, 2, -3)\}$

---

Partial Fractions

The study of rates of change is Calculus. Partial fractions are a technique used in calculus to find a function if its rate of change is knwon.

Decomposition is reversing a process.

For example,

$$\dfrac{x + 14}{(x-4)(x+2)} = \dfrac{3}{x+4} + \dfrac{-2}{x +2}$$

Each fraction on the right is a partial fraction and the sum of these is called the **partial fraction decomposition (PFD) ** of the rational expression on the left-hand side.

PFDs can be written fro rational expressions in the form of

$$\dfrac{P(x)}{Q(x)}$$

Where P and Q have no common factors and the highest power in the numerator is less than te highest power in the denominator.

Lets find the partial fraction decomposition of

$$\dfrac{3x^2 + 17x + 14}{(x-2)(x^2 + 2x + 4)}$$

First we need to set up the PFD with the unknown constants. A constant (A) over the linear factor and a linear expression (Bx + C) over the prime quadratic factor.

$$\dfrac{3x^2 + 17x + 14}{(x-2)(x^2 + 2x + 4)} = \dfrac{A}{x - 2} + \dfrac{Bx + C}{2^2 + 2x + 4}$$

Then we multiply both sides of the resulting equation by the least common denominator (x-2)(x^2 + 2x + 4)

$$(x-2)(x^2 + 2x + 4) \cdot \begin{bmatrix} \dfrac{3x^2 + 17x + 14}{(x-2)(x^2 + 2x + 4)} \end{bmatrix} = (x-2)(x^2 + 2x + 4) \cdot \begin{bmatrix} \dfrac{A}{x - 2} + \dfrac{Bx + C}{2^2 + 2x + 4} \end{bmatrix}$$

Using the distributive property on the left side we get

$$\begin{split} \cancel{(x-2)(x^2 + 2x + 4)} \cdot \begin{bmatrix} \dfrac{3x^2 + 17x + 14}{\cancel{(x-2)(x^2 + 2x + 4)}} \end{bmatrix} &= 3x^2 + 17x + 14 \end{split}$$

Using the distributive property on the right side we get

$$\begin{split} &= (\cancel{x-2})(\bcancel{x^2 + 2x + 4}) \cdot \begin{bmatrix} \dfrac{A}{\cancel{x - 2}} + \dfrac{Bx + C}{\bcancel{x^2 + 2x + 4}} \end{bmatrix} \\ &= \dfrac{A}{x^2 + 2x + 4} + \dfrac{Bx + C}{x - 2} \\ \end{split}$$

And so we are left with

$$3x^2 + 17x + 14 = \dfrac{A}{x^2 + 2x + 4} + \dfrac{Bx + C}{x - 2}$$

Then dividing out common factors in numerators an denominators we get

$$3x^2 + 17x + 14 = A(x^2 + 2x + 4) + (Bx + C)(x - 2)$$

And we can simplify the right side by

$$\begin{split} &= A(x^2 + 2x + 4) + (Bx + C)(x - 2) \\ &= Ax^2 + 2Ax + 4A + Bx^2 - 2Bx + Cx - 2C \\ 3x^2 + 17x + 14 &= (A + B)x^2 + (2A - 2B + C)x + (4A - 2C) \\ \end{split}$$

And now we can see that

$$\begin{split} A + B &= 3 \\ 2A - 2B + C &= 17 \\ 4A - 2C &= 14 \end{split}$$

So we solve the system for A, B and C as we’ve done by solving linear systems of 3 variables previously. We get A = 5, B = -2 and C = 3.

And our PFD is

$$\begin{split} \dfrac{3x^2 + 17x + 14}{(x - 2)(x^2 + 2x + 4)} &= \dfrac{A}{x - 2} + \dfrac{Bx+C}{x^2 + 2x + 4} \\ &= \dfrac{5}{x-2} + \dfrac{-2x + 3}{x^2 + 2x + 4} \\ \end{split}$$

---

Systems of Nonlinear Equations in Two Variables — 02/06/2024

A nonlinear system contains at least one equation that cannot be expressed in the form Ax + By = C, e.g. $x^2 = 2y + 10$ bc $x^2$ is not linear.

A solution of a nonlinear system in two vars is an ordered pair of real numbers that satisfies both equations in the system. The solution set (if there is one) corresponds to the intersection points(s) of the graphs of the equations in the system. Nonlinear systems can be circles, parabolas, or anything other than two lines.

We can solve nonlinear systems using the addition and substituation method from solving linear systems.

However, to solve with the addition method if each equation is in the form of $Ax^2 + By^2 = C$. The substituation method remains the same as linear systems.

For example,

$$\begin{split} 4x^2 + y^2 &= 13 \\ x^2 + y^2 &= 10 \end{split}$$

Since both equations are squared theres no need to convert one to a squared equation.

So we start off by multiplying the 2nd equation by -1 to turn $y^2 = 0$ to create

$$\begin{split} 4x^2 + y^2 &= 13 \\ - x^2 - y^2 &= - 10 \end{split}$$

Then we add them to make

$$\begin{split} 3x^2 &= 3 \\ x^2 &= 1 \\ \end{split}$$

And use the square root property: if $x^2 = c$ then $x = \pm \sqrt{c}$, to get

$$x = \pm 1$$

Then we back-substitute to find the other var

$$\begin{split} 1^2 + y^2 &= 10 \\ y^2 &= 9 \\ y &= \pm 3 \\ \end{split}$$

And so, (1, 3) and (1, -3) are our solutions if x = -1

---

Matrices and Determinants

Matrices are how we are able to view and share images on the internet.

A matrix can be defied as a capital letter, e.g. A

$$A = \lbrack a_{ij}\rbrack$$

• i is it’s row number
• j is it’s column number

If i = j then it is a square matrix. For example $$A = \lbrack a_{22}\rbrack$$ could be represented as and the “id” of $a_{22}$ would be 1

$$A = \begin{bmatrix} 5 & y+1 \\ z & 1 \end{bmatrix}$$

Addition and Subtraction

Matrix addition, $A + B = \lbrack a_ij + b_ij\rbrack$, is really just adding the corresponding elements together. And then vice versa for subtraction.

$$\begin{bmatrix} 5 & 3 \\ 2 & 1 \end{bmatrix} + \begin{bmatrix} 2 & 4 \\ 6 & 5 \end{bmatrix} = \begin{bmatrix} 7 & 7 \\ 8 & 6 \end{bmatrix}$$

A matrix that has all elements equal to 0 is called a zero matrix. If A is an m * x matrix and the zero matrix is as well then A + 0 = A, e.g,

$$\begin{bmatrix} 5 & 3 \\ 2 & 1 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 5 & 3 \\ 2 & 1 \end{bmatrix}$$

Scalar Multiplication

A matrix of order 1 * 1, such as [6], only has 1 entry is called a scalar aka real numbers.

The distributive property of algebra apply to scalar multiplication.

For example, $cA = \lbrack ca_{ij}\rbrack$

$$2 \begin{bmatrix} 5 & 3 \\ 2 & 1 \end{bmatrix} = \begin{bmatrix} 10 & 6 \\ 4 & 2 \end{bmatrix}$$

Matrix Multiplication

This is a bit counter intuitive, but we don’t multiply two matrices by multiplying the corresponding entries of matrices. Instead, we multiply as a row-by-column format.

For example,

$$AB = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} e & f \\ g & h \end{bmatrix}$$

So the order of operations would be:

$$\begin{split} \begin{bmatrix} a & b \\ & \\ \end{bmatrix} \cdot \begin{bmatrix} e & \\ g & \end{bmatrix} &= \begin{bmatrix} ae + bg & \\ & \\ \end{bmatrix} \\ \begin{bmatrix} & \\ c & d \\ \end{bmatrix} \cdot \begin{bmatrix} e & \\ g & \end{bmatrix} &= \begin{bmatrix} ae + bg & \\ ce+dg & \\ \end{bmatrix} \\ \begin{bmatrix} a & b \\ & \\ \end{bmatrix} \cdot \begin{bmatrix} & f \\ & h \end{bmatrix} &= \begin{bmatrix} ae + bg & af + bh \\ ce+dg & \\ \end{bmatrix} \\ AB = \begin{bmatrix} & \\ c & d \\ \end{bmatrix} \cdot \begin{bmatrix} & f \\ & h \end{bmatrix} &= \begin{bmatrix} ae + bg & af + bh \\ ce+dg & cf+dh \\ \end{bmatrix} \\ \end{split}$$

A formal definition of the product of two matrices is the number of columns of the first matrix must equal the number of rows of the second matrix,

$$mn \cdot np$$

Where $m \cdot p$ is the order of AB and $n \cdot n$ must be equal.

Multiplicitive Inverse

The multiplicative inverse is the reciporcal of a matrix!

They’re used to solve linear equations and in calculus for differentiation and integration involving rational and power functions w/ negative exponents.

We can define the multiplicative inverse as

$$A^{-1} = \dfrac{1}{ad - bc} \begin{bmatrix} d & -d \\ -c & a \\ \end{bmatrix}$$

For example, the inverse of

$$\begin{split} A = \begin{bmatrix} 7 & 2 \\ 17 & 5 \\ \end{bmatrix} \end{split}$$

Would be

$$\begin{split} A^{-1} &= \dfrac{1}{5(7) - 2(17)} \begin{bmatrix} 5 & -2 \\ -17 & 7 \\ \end{bmatrix} \\ &= \dfrac{1}{35 - 34} \begin{bmatrix} 5 & -2 \\ -17 & 7 \\ \end{bmatrix} \\ &= \dfrac{1}{1} \begin{bmatrix} 5 & -2 \\ -17 & 7 \\ \end{bmatrix} \\ &= \begin{bmatrix} 5 & -2 \\ -17 & 7 \\ \end{bmatrix} \\ \end{split}$$

And so we can get the multiplicative identity matrix by, aka the inverse of matrix A

$$\begin{split} A \cdot A^{-1} &= I_2 \\ I_2 &= \begin{bmatrix} 7 & 2 \\ 17 & 5 \\ \end{bmatrix} \begin{bmatrix} 5 & -2 \\ -17 & 7 \\ \end{bmatrix} \\ &= \begin{bmatrix} 7(5) + 2(-17) & 7(-2) + 2(7) \\ 17(5) + 5(-17) & 17(-2) + 5(7) \end{bmatrix} \\ &= \begin{bmatrix} 35 - 34 & -14 + 14 \\ 85 - 85 & -34 + 35 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ \end{split}$$

---

Determinants

A determinant is a function of the entries of only square matrices. It is the scaling factor, telling us how the matrix scales areas/volumes.

The determinant of the matrix $\begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{bmatrix}$ is denoted by $\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{vmatrix}$ and is defined by

$$\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{vmatrix} = a_1b_2 - a_2b_1$$

---

For determinants w/ the the order of 3 lets do an example,

$$\begin{split} \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \\ \end{vmatrix} \end{split}$$

The first thing we want to do is get rid of the first row and the first column from $a_1$

$$\begin{split} \begin{bmatrix} \cancel{a_1} & \cancel{b_1} & \cancel{c_1} \\ \cancel{a_2} & b_2 & c_2 \\ \cancel{a_3} & b_3 & c_3 \\ \end{bmatrix} &= a_1 \begin{bmatrix} b_2 & c_2 \\ b_3 & c_3 \\ \end{bmatrix} \end{split}$$

Then next one will be canceling from $b_1$

$$\begin{split} \begin{bmatrix} \cancel{a_1} & \cancel{b_1} & \cancel{c_1} \\ a_2 & \cancel{b_2} & c_2 \\ a_3 & \cancel{b_3} & c_3 \\ \end{bmatrix} &= b_1 \begin{bmatrix} a_2 & c_2 \\ a_3 & c_3 \\ \end{bmatrix} \end{split}$$

Then finally canceling from $c_1$

$$\begin{split} \begin{bmatrix} \cancel{a_1} & \cancel{b_1} & \cancel{c_1} \\ a_2 & b_2 & \cancel{c_2} \\ a_3 & b_3 & \cancel{c_3} \\ \end{bmatrix} = c_1 \begin{bmatrix} a_2 & b_2 \\ a_3 & b_3 \\ \end{bmatrix} \end{split}$$

Then we combine them together to form

$$\begin{split} \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \\ \end{vmatrix} &= a_1 \begin{bmatrix} b_2 & c_2 \\ b_3 & c_3 \\ \end{bmatrix} - b_1 \begin{bmatrix} a_2 & c_2 \\ a_3 & c_3 \\ \end{bmatrix} + c_1 \begin{bmatrix} a_2 & b_2 \\ a_3 & b_3 \\ \end{bmatrix} \end{split}$$

---

What about an nth order determinant, n * n matrices? These are those w/ n > 2.

Lets do an example,

$$\begin{split} \begin{vmatrix} 1 & 0 & 0 & -6 \\ 2 & 5 & 0 & 3 \\ -1 & 2 & 3 & 5 \\ 2 & 1 & -2 & 3 \\ \end{vmatrix} \end{split}$$

First you want to find the row or column with the most amount of zeros bc we’re gonna turn this big one into smaller ones and since we multiply the coefficient by the new mini matrix we’re effectively removing workload as 0 multiply a matrix is 0.

So we will choose the first row since it has 2 zeros.

Our first colum to eliminate will be $1$

$$\begin{split} \begin{bmatrix} \cancel{1} & \cancel{0} & \cancel{0} & \cancel{-6} \\ \cancel{2} & 5 & 0 & 3 \\ \cancel{-1} & 2 & 3 & 5 \\ \cancel{2} & 1 & -2 & 3 \\ \end{bmatrix} = 1 \begin{bmatrix} 5 & 0 & 3 \\ 2 & 3 & 5 \\ 1 & -2 & 3 \\ \end{bmatrix} \end{split}$$

Then the 2nd column by $0$

$$\begin{split} \begin{bmatrix} \cancel{1} & \cancel{0} & \cancel{0} & \cancel{-6} \\ 2 & \cancel{5} & 0 & 3 \\ -1 & \cancel{2} & 3 & 5 \\ 2 & \cancel{1} & -2 & 3 \\ \end{bmatrix} = 0 \begin{bmatrix} 2 & 0 & 3 \\ -1 & 3 & 5 \\ 2 & -2 & 3 \\ \end{bmatrix} = 0 \end{split}$$

Now the 3rd column will result in zero too so we’ll skip it and move onto the last, $6$

$$\begin{split} \begin{bmatrix} \cancel{1} & \cancel{0} & \cancel{0} & \cancel{-6} \\ 2 & 5 & 0 & \cancel{3} \\ -1 & 2 & 3 & \cancel{5} \\ 2 & 1 & -2 & \cancel{3} \\ \end{bmatrix} = -6 \begin{bmatrix} 2 & 5 & 0 \\ -1 & 2 & 3 \\ 2 & 2 & -2 \\ \end{bmatrix} \end{split}$$

And so our expression becomes a repeated +, -, +, -, etc

$$\begin{split} \begin{vmatrix} 1 & 0 & 0 & -6 \\ 2 & 5 & 0 & 3 \\ -1 & 2 & 3 & 5 \\ 2 & 1 & -2 & 3 \\ \end{vmatrix} &= 1 \begin{bmatrix} 5 & 0 & 3 \\ 2 & 3 & 5 \\ 1 & -2 & 3 \\ \end{bmatrix} - 0 + 0 - (-6) \begin{bmatrix} 2 & 5 & 0 \\ -1 & 2 & 3 \\ 2 & 2 & -2 \\ \end{bmatrix} \\ &= \begin{bmatrix} 5 & 0 & 3 \\ 2 & 3 & 5 \\ 1 & -2 & 3 \\ \end{bmatrix} 6 \begin{bmatrix} 2 & 5 & 0 \\ -1 & 2 & 3 \\ 2 & 2 & -2 \\ \end{bmatrix} \\ \end{split}$$

So now we have to go further down by converting the 3x3 matrices into 2x2s.

$$\begin{split} \begin{bmatrix} 5 & 0 & 3 \\ 2 & 3 & 5 \\ 1 & -2 & 3 \\ \end{bmatrix} &= 5 \begin{bmatrix} 3 & 5 \\ -2 & 3 \\ \end{bmatrix} \cancel{-0 \begin{bmatrix} 2 & 5 \\ 1 & 3 \\ \end{bmatrix}} +3 \begin{bmatrix} 2 & 3 \\ 1 & -2 \\ \end{bmatrix} \\ &= 5((3\cdot 3) - (-2 \cdot 5)) - 0 + 3((2 \cdot -2) - (1 \cdot 3)) \\ &= 5(9 - (-10)) + 3(-4 - 3) \\ &= 5(19) + 3(-7) \\ &= 95 + (-21) \\ &= 74 \\ \end{split}$$

And

$$\begin{split} \begin{bmatrix} 2 & 5 & 0 \\ -1 & 2 & 3 \\ 2 & 2 & -2 \\ \end{bmatrix} &= 2 \begin{bmatrix} 2 & 3 \\ 1 & -2 \\ \end{bmatrix} -5 \begin{bmatrix} -1 & 3 \\ 2 & -2 \\ \end{bmatrix} \cancel{+ 0 \begin{bmatrix} -1 & 2 \\ 2 & 2 \\ \end{bmatrix}} \\ &= 2((2\cdot-2) + (1 \cdot 3)) - 5((-1\cdot-2) + (3\cdot 2)) + 0 \\ &= 2(-4 - 3) - 5(2 - 6) \\ &= 2(-7) - 5(-4)\\ &= -14 + 20 \\ &= 6 \\ \end{split}$$

And our final result is

$$\begin{split} \begin{vmatrix} 1 & 0 & 0 & -6 \\ 2 & 5 & 0 & 3 \\ -1 & 2 & 3 & 5 \\ 2 & 1 & -2 & 3 \\ \end{vmatrix} &= 1(74) - 0 + 0 - (-6)(6) \\ &= 1(74) + 6(6) \\ &= 74 + 36 \\ &= 110 \\ \end{split}$$